Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.

HalloAHS: Führe deine erste analoge Hamiltonsche Simulation aus

Dieser Abschnitt enthält Informationen zur Ausführung Ihrer ersten analogen Hamilton-Simulation.

Interagierende Spin-Kette

Als kanonisches Beispiel für ein System aus vielen wechselwirkenden Teilchen betrachten wir einen Ring mit acht Spins (von denen sich jeder in den Zuständen „oben“ ↑ und „unten“ ↓⟩ befinden kann). Dieses Modellsystem ist zwar klein, weist aber bereits eine Handvoll interessanter Phänomene natürlich vorkommender magnetischer Materialien auf. In diesem Beispiel werden wir zeigen, wie man eine sogenannte antiferromagnetische Ordnung erzeugt, bei der aufeinanderfolgende Spins in entgegengesetzte Richtungen zeigen.

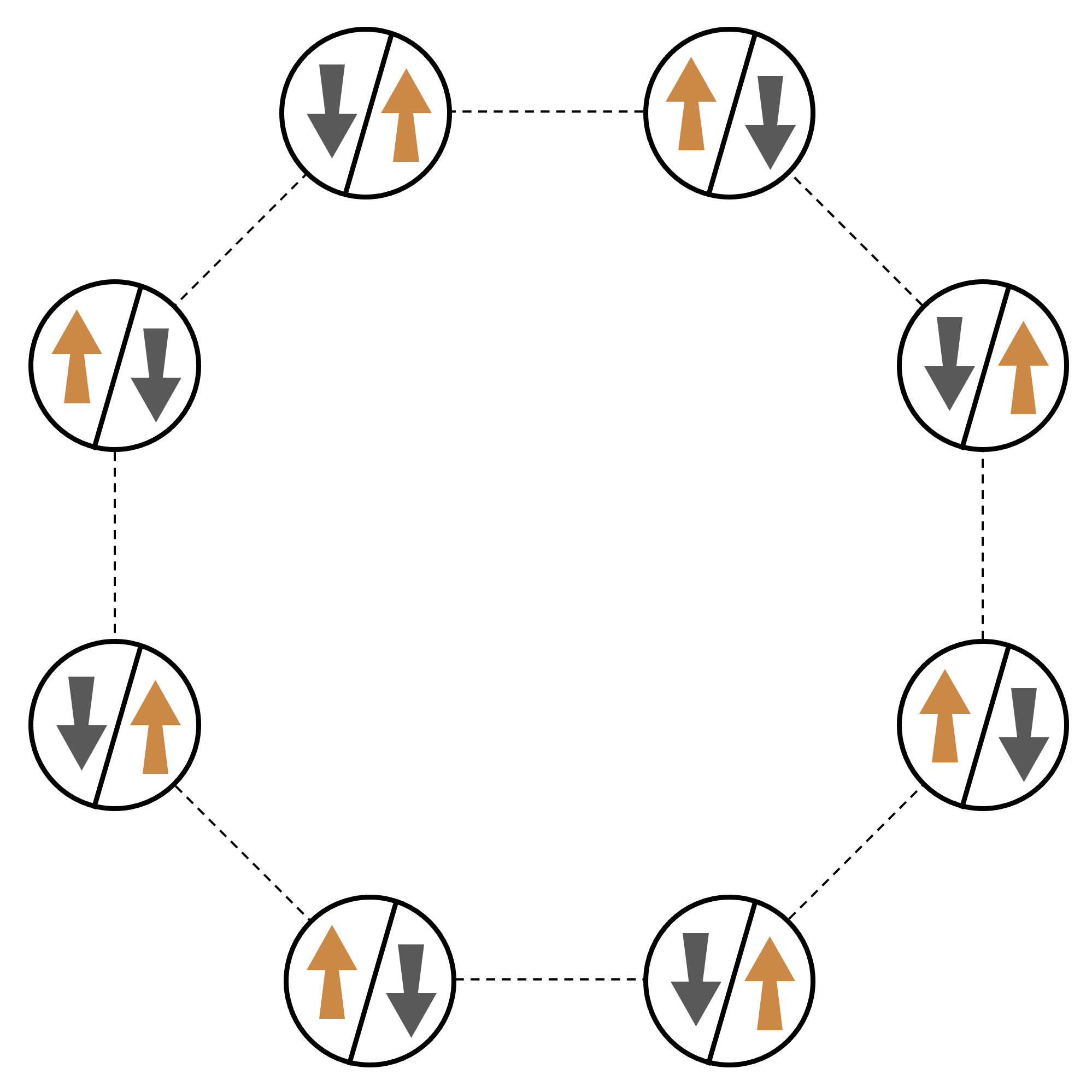
Anordnung

Wir verwenden ein neutrales Atom, das für jeden Spin steht, und die Spinzustände „hoch“ und „runter“ werden jeweils im angeregten Rydberg-Zustand und im Grundzustand der Atome kodiert. Zuerst erstellen wir die 2-D-Anordnung. Wir können den obigen Ring von Spins mit dem folgenden Code programmieren.

Voraussetzungen: Sie müssen das SDKBraket per Pip installieren. (Wenn Sie eine von Braket gehostete Notebook-Instanz verwenden, SDK ist diese zusammen mit den Notebooks vorinstalliert.) Um die Plots zu reproduzieren, müssen Sie matplotlib auch separat mit dem Shell-Befehl installieren. pip install matplotlib

import numpy as np
   import matplotlib.pyplot as plt  # required for plotting
   
   from braket.ahs.atom_arrangement import AtomArrangement
   
   a = 5.7e-6  # nearest-neighbor separation (in meters)
   
   register = AtomArrangement()
   register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

womit wir auch plotten können

fig, ax = plt.subplots(1, 1, figsize=(7,7))
   xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
   ax.plot(xs, ys, 'r.', ms=15)
   for idx, (x, y) in enumerate(zip(xs, ys)):
       ax.text(x, y, f" {idx}", fontsize=12)
   plt.show()  # this will show the plot below in an ipython or jupyter session

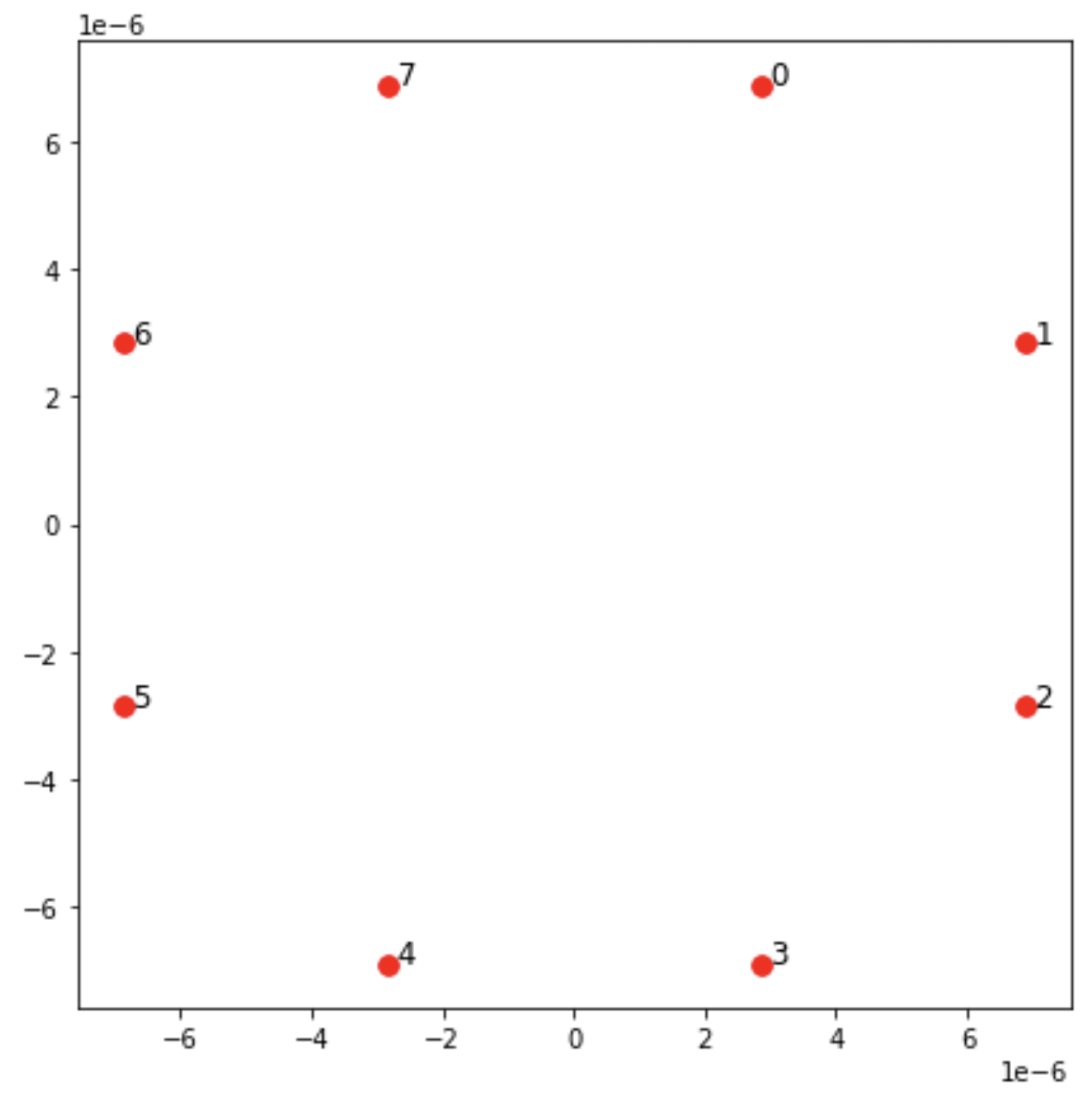
Interaktionen

Um die antiferromagnetische Phase vorzubereiten, müssen wir Wechselwirkungen zwischen benachbarten Spins induzieren. Wir nutzen dafür die Van-der-Waals-Wechselwirkung, die nativ von neutralen Atomgeräten implementiert wird (wie dem Aquila Gerät von QuEra). Unter Verwendung der Spindarstellung kann der Hamiltonsche Term für diese Wechselwirkung als Summe über alle Spinpaare (j, k) ausgedrückt werden.

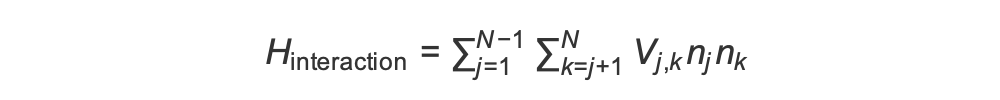
In diesem Fall ist nj=↑ bung↑ _j ein _j Operator, der den Wert 1 nur annimmt, wenn sich Spin j im Zustand „up“ befindet, andernfalls 0. Die Stärke ist V _j,k =C₆/(d_j,k​) ⁶, wobei C ₆ der feste Koeffizient und d der euklidische Abstand zwischen den Spins j und k _j,k ist. Der unmittelbare Effekt dieses Wechselwirkungsterms besteht darin, dass jeder Zustand, in dem sowohl Spin j als auch Spin k „oben“ sind, eine erhöhte Energie (um den Betrag V) aufweist. _j,k Durch die sorgfältige Gestaltung des restlichen AHS Programms wird durch diese Wechselwirkung verhindert, dass sich benachbarte Spins beide im „Up-Zustand“ befinden — ein Effekt, der allgemein als „Rydberg-Blockade“ bekannt ist.

Fahrfeld

Zu Beginn des AHS Programms beginnen alle Spins (standardmäßig) in ihrem „down“ -Zustand, sie befinden sich in einer sogenannten ferromagnetischen Phase. Mit Blick auf unser Ziel, die antiferromagnetische Phase vorzubereiten, spezifizieren wir ein zeitabhängiges kohärentes Antriebsfeld, das die Spins sanft von diesem Zustand in einen Vielteilchenzustand überführt, in dem der Zustand „oben“ bevorzugt wird. Der entsprechende Hamilton-Operator kann geschrieben werden als

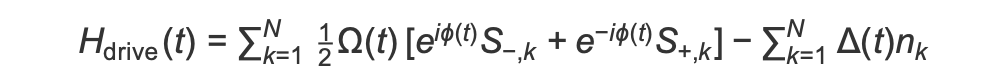
wobei Ω (t), φ (t), δ (t) die zeitabhängige globale Amplitude (auch bekannt als Rabi-Frequenz), Phase und Verstimmung des treibenden Feldes sind, die alle Spins gleichmäßig beeinflussen. Hier sind S _−,k =↓ _k​ bung↑ _k und S _+,k =( S_−,k) ^† =↑ _k​ Chesinik↓ _k die senkenden und anhebenden Operatoren von Spin k, und n _k =↑ _k ↑ ←↑ _k ist derselbe Operator wie zuvor. Der Ω Teil des Antriebsfeldes verbindet kohärent die Zustände „nach unten“ und „nach oben“ aller Spins gleichzeitig, während der Δ-Teil die Energiebelohnung für den Zustand „hoch“ steuert.

Um einen reibungslosen Übergang von der ferromagnetischen Phase zur antiferromagnetischen Phase zu programmieren, spezifizieren wir das treibende Feld mit dem folgenden Code.

from braket.timings.time_series import TimeSeries
   from braket.ahs.driving_field import DrivingField
   
   # smooth transition from "down" to "up" state
   time_max = 4e-6  # seconds
   time_ramp = 1e-7  # seconds
   omega_max = 6300000.0  # rad / sec
   delta_start = -5 * omega_max
   delta_end = 5 * omega_max
   
   omega = TimeSeries()
   omega.put(0.0, 0.0)
   omega.put(time_ramp, omega_max)
   omega.put(time_max - time_ramp, omega_max)
   omega.put(time_max, 0.0)
   
   delta = TimeSeries()
   delta.put(0.0, delta_start)
   delta.put(time_ramp, delta_start)
   delta.put(time_max - time_ramp, delta_end)
   delta.put(time_max, delta_end)
   
   phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)
   
   drive = DrivingField(
       amplitude=omega,
       phase=phi,
       detuning=delta
   )

Wir können die Zeitreihen des Fahrfeldes mit dem folgenden Skript visualisieren.

fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)
   
   ax = axes[0]
   time_series = drive.amplitude.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Omega [rad/s]')
   
   ax = axes[1]
   time_series = drive.detuning.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Delta [rad/s]')
   
   ax = axes[2]
   time_series = drive.phase.time_series
   # Note: time series of phase is understood as a piecewise constant function
   ax.step(time_series.times(), time_series.values(), '.-', where='post');
   ax.set_ylabel('phi [rad]')
   ax.grid()
   ax.set_xlabel('time [s]')
   
   plt.show()  # this will show the plot below in an ipython or jupyter session

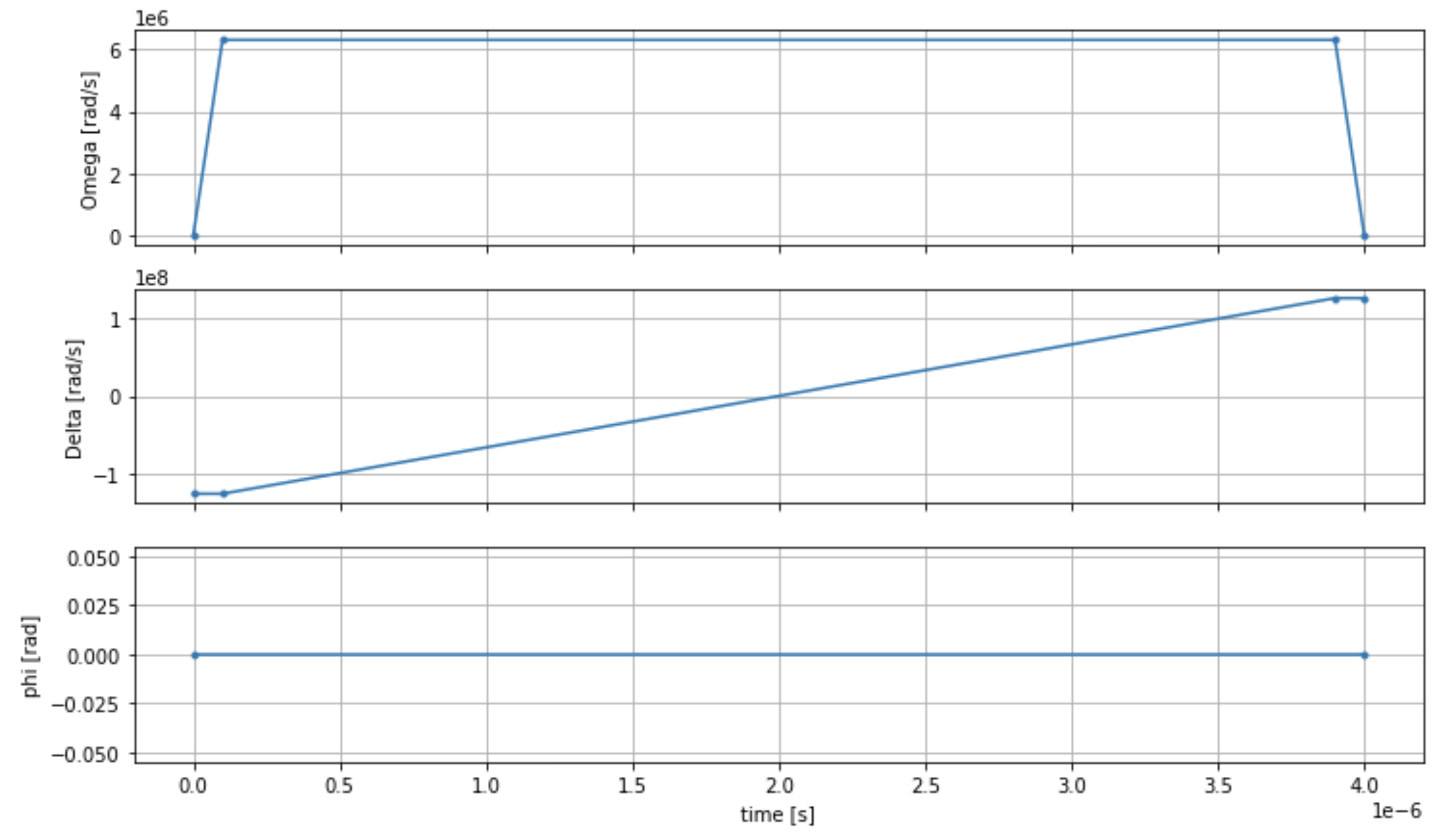
AHSProgramm

Das Register, das treibende Feld (und die impliziten Van-der-Waals-Interaktionen) bilden das Programm Analoge Hamiltonsche Simulation. ahs_program

from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation
   
   ahs_program = AnalogHamiltonianSimulation(
       register=register,
       hamiltonian=drive
   )

Läuft auf einem lokalen Simulator

Da dieses Beispiel klein ist (weniger als 15 Spins), können wir es vor der Ausführung auf einem AHS -kompatiblen Simulator auf dem lokalen AHS Simulator ausführenQPU, der mit dem Braket geliefert wird. SDK Da der lokale Simulator mit dem Braket kostenlos verfügbar ist, ist dies die beste MethodeSDK, um sicherzustellen, dass unser Code korrekt ausgeführt werden kann.

Hier können wir die Anzahl der Aufnahmen auf einen hohen Wert setzen (z. B. 1 Million), weil der lokale Simulator die zeitliche Entwicklung des Quantenzustands verfolgt und Proben aus dem Endzustand zieht. Dadurch wird die Anzahl der Aufnahmen erhöht, während die Gesamtlaufzeit nur geringfügig erhöht wird.

from braket.devices import LocalSimulator
   device = LocalSimulator("braket_ahs")
   
   result_simulator = device.run(
       ahs_program,
       shots=1_000_000
   ).result()  # takes about 5 seconds

Analysieren der Simulatorergebnisse

Wir können die Schussergebnisse mit der folgenden Funktion aggregieren, die den Status jedes Spins ableitet (der „d“ für „runter“, „u“ für „oben“ oder „e“ für leere Stelle sein kann) und zählt, wie oft jede Konfiguration in den Schüssen aufgetreten ist.

from collections import Counter
   
   def get_counts(result):
       """Aggregate state counts from AHS shot results
   
       A count of strings (of length = # of spins) are returned, where
       each character denotes the state of a spin (site):
          e: empty site
          u: up state spin
          d: down state spin
   
       Args:
          result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)
   
       Returns
           dict: number of times each state configuration is measured
   
       """
       state_counts = Counter()
       states = ['e', 'u', 'd']
       for shot in result.measurements:
           pre = shot.pre_sequence
           post = shot.post_sequence
           state_idx = np.array(pre) * (1 + np.array(post))
           state = "".join(map(lambda s_idx: states[s_idx], state_idx))
           state_counts.update((state,))
       return dict(state_counts)
   
   counts_simulator = get_counts(result_simulator)  # takes about 5 seconds
   print(counts_simulator)

{'udududud': 330944, 'dudududu': 329576, 'dududdud': 38033, ...}

Hier counts ist ein Wörterbuch, das zählt, wie oft jede Zustandskonfiguration in den einzelnen Schüssen beobachtet wurde. Wir können sie auch mit dem folgenden Code visualisieren.

from collections import Counter
   
   def has_neighboring_up_states(state):
       if 'uu' in state:
           return True
       if state[0] == 'u' and state[-1] == 'u':
           return True
       return False
   
   def number_of_up_states(state):
       return Counter(state)['u']
   
   def plot_counts(counts):
       non_blockaded = []
       blockaded = []
       for state, count in counts.items():
           if not has_neighboring_up_states(state):
               collection = non_blockaded
           else:
               collection = blockaded
           collection.append((state, count, number_of_up_states(state)))
   
       blockaded.sort(key=lambda _: _[1], reverse=True)
       non_blockaded.sort(key=lambda _: _[1], reverse=True)
   
       for configurations, name in zip((non_blockaded,
                                       blockaded),
                                       ('no neighboring "up" states',
                                       'some neighboring "up" states')):
           plt.figure(figsize=(14, 3))
           plt.bar(range(len(configurations)), [item[1] for item in configurations])
           plt.xticks(range(len(configurations)))
           plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
           plt.ylabel('shots')
           plt.grid(axis='y')
           plt.title(f'{name} configurations')
           plt.show()
   
   plot_counts(counts_simulator)

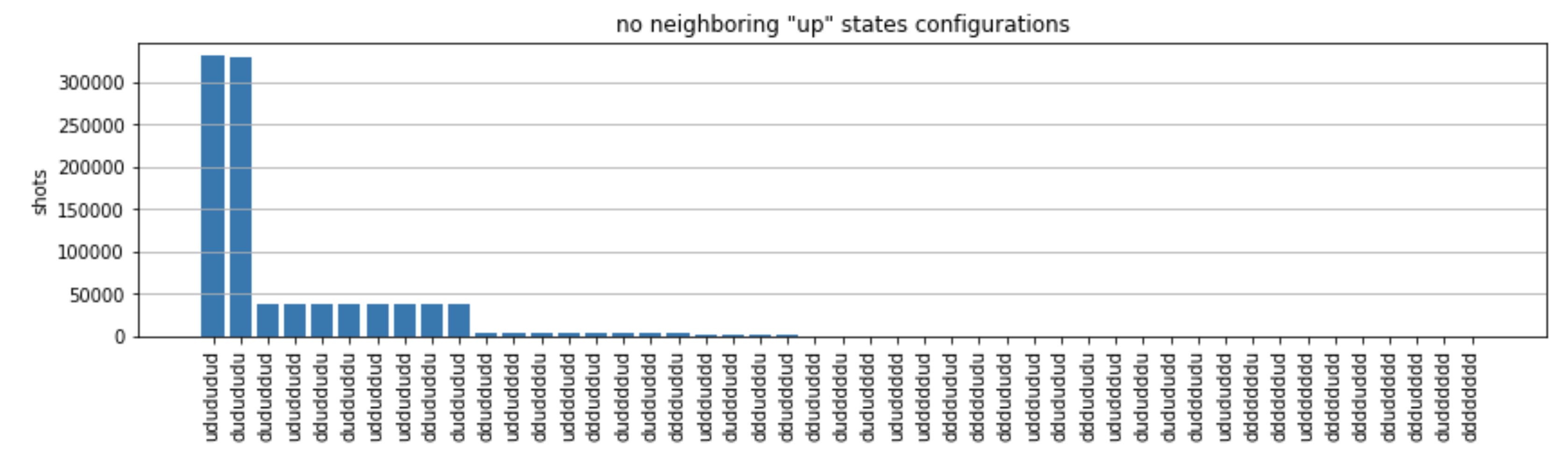
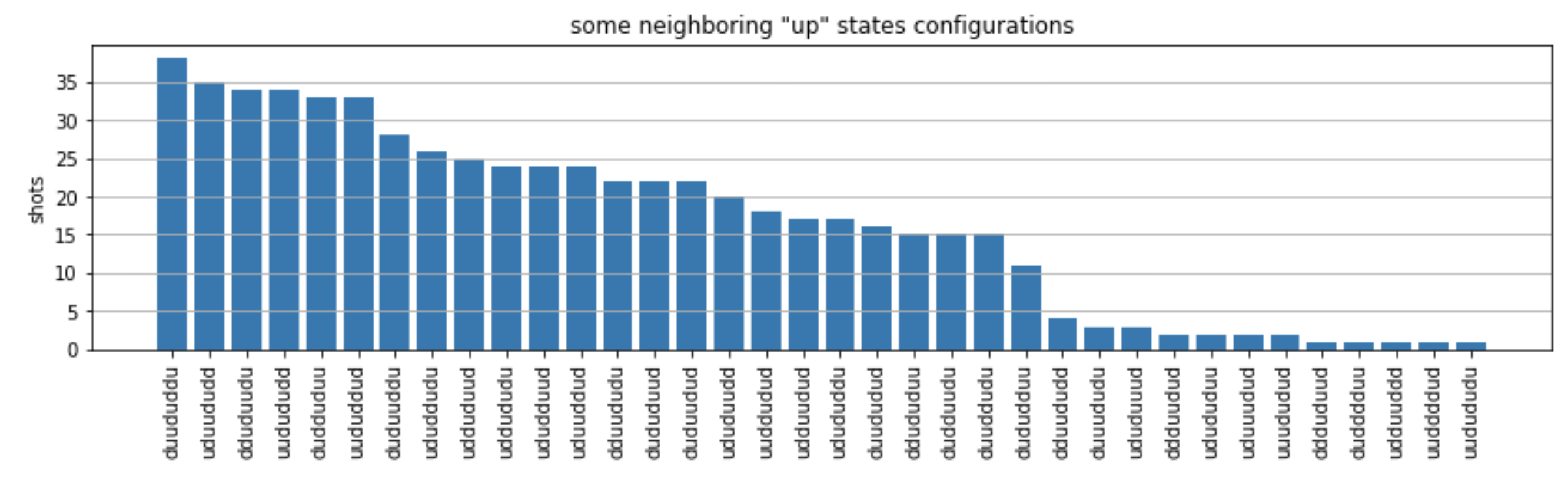
Aus den Diagrammen können wir die folgenden Beobachtungen ablesen, die belegen, dass wir die antiferromagnetische Phase erfolgreich vorbereitet haben.

Aquila läuft weiter QuEra QPU

Voraussetzungen: Wenn Sie neu bei Amazon Braket sind SDK, stellen Sie bitte sicher, dass Sie neben der Pip-Installation von Braket auch die erforderlichen Schritte für Erste Schritte abgeschlossen haben.

Wenn alle Abhängigkeiten installiert sind, können wir uns mit dem verbinden Aquila QPU.

from braket.aws import AwsDevice
   
   aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

Um unser AHS Programm geeignet zu machen für QuEra Bei der Maschine müssen wir alle Werte runden, um die von der Maschine erlaubte Genauigkeit einzuhalten Aquila QPU. (Diese Anforderungen werden durch die Geräteparameter bestimmt, deren Name „Auflösung“ enthält. Wir können sie sehen, indem wir sie aquila_qpu.properties.dict() in einem Notizbuch ausführen. Weitere Informationen zu den Funktionen und Anforderungen von Aquila finden Sie in der Einführung in das Aquila-Notizbuch.) Wir können das tun, indem wir die discretize Methode aufrufen.

discretized_ahs_program = ahs_program.discretize(aquila_qpu)

Jetzt können wir das Programm (vorerst nur 100 Aufnahmen) auf dem ausführen Aquila QPU.

task = aquila_qpu.run(discretized_ahs_program, shots=100)
   
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")

task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: CREATED

Aufgrund der großen Varianz, wie lange die Ausführung einer Quantenaufgabe dauern kann (abhängig von Verfügbarkeitsfenstern und QPU Auslastung), empfiehlt es sich, die Quantenaufgabe zu notierenARN, damit wir ihren Status zu einem späteren Zeitpunkt mit dem folgenden Codeausschnitt überprüfen können.

# Optionally, in a new python session
   
   from braket.aws import AwsQuantumTask
   
   SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"
   
   task = AwsQuantumTask(arn=SAVED_TASK_ARN)
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")

*[Output]*
   task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: COMPLETED

Sobald der Status lautet COMPLETED (was auch auf der Quantenaufgaben-Seite der Amazon Braket-Konsole überprüft werden kann), können wir die Ergebnisse abfragen mit:

result_aquila = task.result()

Analysieren der Ergebnisse QPU

Mit den gleichen get_counts Funktionen wie zuvor können wir die Anzahl berechnen:

counts_aquila = get_counts(result_aquila)
   print(counts_aquila)

*[Output]*
   {'udududud': 24, 'dudududu': 17, 'dududdud': 3, ...}

und plotten Sie sie mitplot_counts:

plot_counts(counts_aquila)

Beachten Sie, dass ein kleiner Teil der Aufnahmen leere Seiten hat (mit „e“ gekennzeichnet). Dies ist auf eine Unvollkommenheit der Präparation pro Atom von 1— 2% zurückzuführen Aquila QPU. Abgesehen davon stimmen die Ergebnisse innerhalb der erwarteten statistischen Fluktuation aufgrund der geringen Anzahl von Schüssen mit der Simulation überein.

Nächste Schritte

Herzlichen Glückwunsch, Sie haben jetzt Ihren ersten AHS Workload auf Amazon Braket mit dem lokalen AHS Simulator ausgeführt und Aquila QPU.

Um mehr über die Rydberg-Physik, die analoge Hamiltonsche Simulation und die Aquila Gerät finden Sie in unseren Beispiel-Notebooks.