Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.
Asymmetrische Shapley-Werte
Bei der Lösung SageMaker Clarify zur Erklärung von Zeitreihenprognosemodellen handelt es sich um eine Methode der Merkmalszuweisung, die auf der kooperativen Spieltheorie
Hintergrund
Ziel ist es, Zuordnungen von Eingabe-Features zu einem bestimmten Prognosemodell f zu berechnen. Das Prognosemodell verwendet die folgenden Eingaben:
Vergangene Zeitreihen (Ziel TS). Dabei könnte es sich beispielsweise um ehemalige tägliche Zugpassagiere auf der Strecke Paris-Berlin handeln, die mit x gekennzeichnet ist. t
(Optional) Eine kovariate Zeitreihe. Dies könnten beispielsweise Feierlichkeiten und Wetterdaten sein, die mit z t ∈ R S bezeichnet werden. Bei Verwendung könnte die Kovariate TS nur für die vergangenen Zeitschritte oder auch für die future Zeitschritte (im Festkalender enthalten) verfügbar sein.
(Optional) Statische Kovariaten, z. B. Servicequalität (wie 1. oder 2. Klasse), bezeichnet mit u ∈ R E.
Statische Kovariaten, dynamische Kovariaten oder beides können je nach Anwendungsszenario weggelassen werden. Bei einem Prognosehorizont K ≥ 0 (z. B. K=30 Tage) kann die Modellvorhersage durch die Formel charakterisiert werden: f (x[1:T], z[1:T+K], u) = x. [T+1:T +K+1]
Das folgende Diagramm zeigt eine Abhängigkeitsstruktur für ein typisches Prognosemodell. Die Vorhersage zum Zeitpunkt t+1 hängt von den drei zuvor genannten Eingangstypen ab.
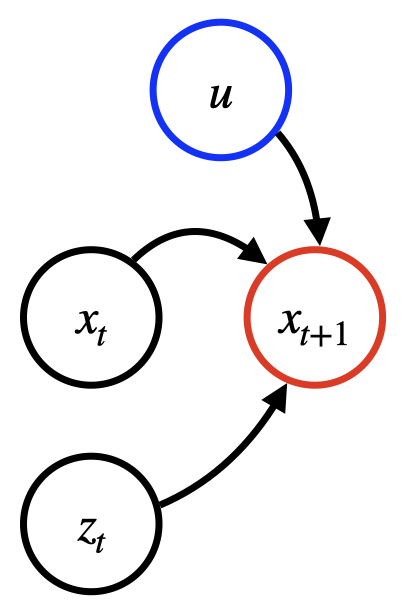
Methode
Erklärungen werden berechnet, indem das Zeitreihenmodell f anhand einer Reihe von Punkten abgefragt wird, die aus der ursprünglichen Eingabe abgeleitet wurden. Anhand spieltheoretischer Konstruktionen werden die Durchschnittswerte der Unterschiede zwischen den Vorhersagen geklärt, wobei Teile der Eingaben iterativ verschleiert (d. h. auf einen Basiswert festgelegt) werden. Durch die zeitliche Struktur kann in chronologischer oder antichronologischer Reihenfolge oder in beidem navigiert werden. Chronologische Erklärungen werden erstellt, indem iterativ Informationen aus dem ersten Zeitschritt hinzugefügt werden, während Informationen aus dem letzten Schritt antichronologisch hinzugefügt werden. Letzteres Modell ist möglicherweise besser geeignet, wenn es um Verzerrungen in jüngster Zeit geht, z. B. bei der Prognose von Aktienkursen. Eine wichtige Eigenschaft der berechneten Erklärungen besteht darin, dass sie in ihrer Summe den Output des ursprünglichen Modells ergeben, wenn das Modell deterministische Ergebnisse liefert.
Resultierende Zuschreibungen
Bei den resultierenden Attributionen handelt es sich um Punktzahlen, die einzelne Beiträge bestimmter Zeitintervalle oder Eingabe-Features zur endgültigen Prognose in jedem prognostizierten Zeitschritt kennzeichnen. Clarify bietet zur Erläuterung die folgenden zwei Granularitäten:
Zeitliche Erklärungen sind kostengünstig und geben nur Auskunft über bestimmte Zeitschritte, z. B. wie viel die Informationen des 19. Tages in der Vergangenheit zur Prognose des ersten Tages in der future beigetragen haben. Diese Zuschreibungen erklären keine individuellen statischen Kovariaten und aggregierten Erklärungen von Ziel- und kovariaten Zeitreihen. Bei den Attributionen handelt es sich um eine Matrix A, wobei jedes A tk die Zuordnung des Zeitschritts t zur Prognose des Zeitschritts T+k darstellt. Beachten Sie, dass t größer als T sein kann, wenn das Modell future Kovariaten akzeptiert.
Präzise Erklärungen sind rechenintensiver und bieten eine vollständige Aufschlüsselung aller Attributionen der Eingabevariablen.
Anmerkung
Feinkörnige Erklärungen unterstützen nur die chronologische Reihenfolge.
Die sich daraus ergebenden Zuschreibungen sind ein Triplett, das sich wie folgt zusammensetzt:
Matrix A x ∈ R T×K bezogen auf die Eingabezeitreihe, wobei A tk x die Zuordnung von x t zum Prognoseschritt T+k ist
Tensor A z ∈ R T+K×S×K bezieht sich auf die kovariate Zeitreihe, wobei A tsk z die Zuordnung von z ts (d. h. der ersten Kovariate TS) zum Prognoseschritt T+k ist
Matrix A u ∈ R E×K bezieht sich auf die statischen Kovariaten, wobei A ek u die Zuordnung von u e (der zehnten statischen Kovariate) zum Prognoseschritt T+k ist
Unabhängig von der Granularität enthält die Erklärung auch einen Offsetvektor B ∈ R K, der das „grundlegende Verhalten“ des Modells darstellt, wenn alle Daten verschleiert sind.