Requisitos del sistema de coordenadas para trabajos de etiquetado Uso de datos de nube de puntos en un sistema de coordenadas universal Fusión de sensores Cálculo de cuaterniones de orientación y posición Transformaciones de fusión de sensores de Ground Truth

Sistemas de coordenadas y fusión de sensores

Los datos de nube de puntos siempre se ubican en un sistema de coordenadas. Este sistema de coordenadas puede ser local para el vehículo o el dispositivo que detecta el entorno, o puede ser un sistema de coordenadas universal. Cuando se utilizan trabajos de etiquetado de nube de puntos 3D de Ground Truth, todas las anotaciones se generan mediante el sistema de coordenadas de datos de entrada. Para algunos tipos de tareas y entidades de tareas de etiquetado, se debe proporcionar datos en un sistema de coordenadas universal.

En este tema, aprenderá lo siguiente:

Cuando deba proporcionar datos de entrada en un sistema de coordenadas mundial o un fotograma de referencia global.
Qué es una coordenada universal y cómo se pueden convertir datos de nube de puntos en un sistema de coordenadas universal.
Cómo puede utilizar sus matrices extrínsecas de sensores y cámaras para proporcionar datos de postura cuando se utiliza la fusión de sensores.

Requisitos del sistema de coordenadas para trabajos de etiquetado

Si los datos de nube de puntos se recopilaron en un sistema de coordenadas local, puede utilizar una matriz extrínseca del sensor utilizado para recopilar los datos y convertirlos en un sistema de coordenadas universal o en un fotograma de referencia global. Si no puede obtener una extrínseca para los datos de nube de puntos y, como resultado, no puede obtener nubes de puntos en un sistema de coordenadas universal, puede proporcionar datos de nube de puntos en un sistema de coordenadas local para la detección de objetos de nube de puntos 3D y los tipos de tareas de segmentación semántica.

Para el rastreo de objetos, debe proporcionar datos de nube de puntos en un sistema de coordenadas universal. Esto se debe a que cuando rastrea objetos a través de múltiples fotogramas, el propio vehículo ego se está moviendo en el mundo y por lo tanto todos los fotogramas necesitan un punto de referencia.

Si incluye datos de cámara para la fusión de sensores, se recomienda proporcionar posturas de cámara en el mismo sistema de coordenadas universal que el sensor 3D (como un sensor LiDAR).

Uso de datos de nube de puntos en un sistema de coordenadas universal

En esta sección se explica lo que es un sistema de coordenadas universal (SCU), también conocido como fotograma de referencia global, y se explica cómo se pueden proporcionar datos de nube de puntos en un sistema de coordenadas universal.

¿Qué es un sistema de coordenadas universal?

Un SCU o fotograma de referencia global es un sistema de coordenadas universal fijo en el que se colocan los sistemas de coordenadas del vehículo y del sensor. Por ejemplo, si se encuentran varios fotogramas de nube de puntos en diferentes sistemas de coordenadas porque se recopilaron a partir de dos sensores, se puede utilizar un SCU para convertir todas las coordenadas de estos fotogramas de nube de puntos en un único sistema de coordenadas, donde todos los fotogramas tienen el mismo origen (0,0,0). Esta transformación se realiza trasladando el origen de cada fotograma al origen del SCU utilizando un vector de traslación y girando los tres ejes (normalmente x, y y z) a la orientación correcta utilizando una matriz de rotación. Esta transformación rígida del cuerpo se llama transformación homogénea.

Un sistema de coordenadas mundial es importante en la planificación de rutas globales, la localización, la cartografía y las simulaciones de escenarios de conducción. Ground Truth utiliza el sistema de coordenadas mundiales cartesianas para diestros, como el definido en la norma ISO 8855, donde el eje x está orientado hacia delante, hacia el movimiento del coche, el eje y está a la izquierda y el eje z apunta hacia arriba desde el suelo.

El fotograma de referencia global depende de los datos. Algunos conjuntos de datos utilizan la posición LiDAR del primer fotograma como origen. En este escenario, todos los fotogramas utilizan el primer fotograma como referencia y el rumbo y la posición del dispositivo estarán cerca del origen en el primer fotograma. Por ejemplo, los conjuntos de datos KITTI tienen el primer fotograma como referencia para las coordenadas universales. Otros conjuntos de datos usan una posición del dispositivo que es diferente del origen.

Tenga en cuenta que este no es el sistema de GPS/IMU coordinate system, which is typically rotated by 90 degrees along the z-axis. If your point cloud data is in a GPS/IMU coordenadas (como los OXT en el conjunto de datos AV KITTI de código abierto), por lo que debe transformar el origen en un sistema de coordenadas mundial (normalmente el sistema de coordenadas de referencia del vehículo). Para aplicar esta transformación, multiplique los datos con métricas de transformación (la matriz de rotación y el vector de traslación). Esto transformará los datos de su sistema de coordenadas original en un sistema de coordenadas de referencia global. Más información sobre esta transformación en la siguiente sección.

Convertir datos de nube de puntos 3D en un SCU

Ground Truth supone que los datos de nube de puntos ya se han transformado en un sistema de coordenadas de referencia de su elección. Por ejemplo, puede elegir el sistema de coordenadas de referencia del sensor (como LiDAR) como sistema de coordenadas de referencia global. También puede tomar nubes de puntos de varios sensores y transformarlas desde la vista del sensor a la vista del sistema de coordenadas de referencia del vehículo. Utilice la matriz extrínseca de un sensor, formada por una matriz de rotación y un vector de traslación, para convertir los datos de nube de puntos en un SCU o fotograma de referencia global.

En conjunto, el vector de traslación y la matriz de rotación se pueden utilizar para crear una matriz extrínseca, que se puede utilizar para convertir datos desde un sistema de coordenadas local a un SCU. Por ejemplo, su matriz extrínseca LiDAR puede estar compuesta como se indica a continuación, donde R es la matriz de rotación y T es el vector de traslación:


LiDAR_extrinsic = [R T;0 0 0 1]

Por ejemplo, el conjunto de datos KITTI de conducción autónoma incluye una matriz de rotación y un vector de traslación para la matriz de transformación extrínseca LiDAR para cada fotograma. El módulo python pykitti se puede utilizar para cargar los datos KITTI, y en el conjunto de datos dataset.oxts[i].T_w_imu proporciona la transformación extrínseca LiDAR para el fotograma i que se puede multiplicar con puntos en ese fotograma para convertirlos en un fotograma universal - np.matmul(lidar_transform_matrix, points). Multiplicar un punto en el fotograma de LiDAR con una matriz extrínseca LiDAR lo transforma en coordenadas universales. Al multiplicar un punto en el fotograma universal con la matriz extrínseca de la cámara, se proporciona las coordenadas de punto en el fotograma de referencia de la cámara.

En el ejemplo de código siguiente se muestra cómo se pueden convertir fotogramas de nube de puntos del conjunto de datos KITTI en un SCU.


import pykitti
import numpy as np

basedir = '/Users/nameofuser/kitti-data'
date = '2011_09_26'
drive = '0079'

# The 'frames' argument is optional - default: None, which loads the whole dataset.
# Calibration, timestamps, and IMU data are read automatically. 
# Camera and velodyne data are available via properties that create generators
# when accessed, or through getter methods that provide random access.
data = pykitti.raw(basedir, date, drive, frames=range(0, 50, 5))

# i is frame number
i = 0

# lidar extrinsic for the ith frame
lidar_extrinsic_matrix = data.oxts[i].T_w_imu

# velodyne raw point cloud in lidar scanners own coordinate system
points = data.get_velo(i)

# transform points from lidar to global frame using lidar_extrinsic_matrix
def generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix):
    tps = []
    for point in points:
        transformed_points = np.matmul(lidar_extrinsic_matrix, np.array([point[0], point[1], point[2], 1], dtype=np.float32).reshape(4,1)).tolist()
        if len(point) > 3 and point[3] is not None:
            tps.append([transformed_points[0][0], transformed_points[1][0], transformed_points[2][0], point[3]])
       
    return tps
    
# customer transforms points from lidar to global frame using lidar_extrinsic_matrix
transformed_pcl = generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix)

Fusión de sensores

Ground Truth admite la fusión de sensores de datos de nube de puntos con hasta 8 entradas de cámara de vídeo. Esta función permite a los etiquetadores humanos ver el fotograma de la nube de puntos en 3D side-by-side con el fotograma de vídeo sincronizado. Además de proporcionar más contexto visual para el etiquetado, la fusión de sensores permite a los trabajadores ajustar anotaciones en la escena 3D y en imágenes 2D y el ajuste se proyecta en la otra vista. El siguiente vídeo muestra un trabajo de etiquetado de nube de puntos 3D con LiDAR y fusión de sensores de cámara.

Para obtener los mejores resultados, al utilizar la fusión de sensores, la nube de puntos debe estar en un WCS. Ground Truth utiliza la información de su sensor (como LiDAR), la cámara y la postura del vehículo ego para calcular matrices extrínsecas e intrínsecas para la fusión de sensores.

Matriz extrínseca

Ground Truth utiliza matrices extrínsecas de los sensores (como LiDAR) e intrínsecas y extrínsecas de las cámaras para proyectar objetos hacia y desde el fotograma de referencia de los datos de nube de puntos al fotograma de referencia de la cámara.

Por ejemplo, para proyectar una etiqueta desde la nube de puntos 3D al plano de imagen de la cámara, Ground Truth transforma puntos 3D desde el sistema de coordenadas propio de LiDAR al sistema de coordenadas de la cámara. Por lo general, esto se hace transformando primero los puntos 3D del sistema de coordenadas propio del LiDAR en un sistema de coordenadas mundial (o un fotograma de referencia global) utilizando la matriz extrínseca de LiDAR. Luego, Ground Truth utiliza la cámara extrínseca inversa (que convierte los puntos de un fotograma de referencia global al fotograma de referencia de la cámara) para transformar los puntos 3D del sistema de coordenadas mundial obtenido en el paso anterior en el plano de imagen de la cámara. La matriz extrínseca LiDAR también se puede utilizar para transformar datos 3D en un sistema de coordenadas universal. Si sus datos 3D ya se han transformado en sistema de coordenadas universal, la primera transformación no tiene ningún impacto en la traslación de etiquetas, y la traslación de etiquetas solo depende de la extrínseca inversa de la cámara. Una matriz de vista se utiliza para visualizar etiquetas proyectadas. Para obtener más información sobre estas transformaciones y la matriz de vistas, consulte Transformaciones de fusión de sensores de Ground Truth.

Ground Truth calcula estas matrices extrínsecas utilizando LiDAR y los datos de posturas de la cámara que proporcione: heading (en cuaterniones: qx, qy, qz y qw) y position (x, y, z). Para el vehículo, normalmente el rumbo y la posición se describen en el fotograma del vehículo en un sistema de coordenadas universal y se llaman postura de vehículo ego. Para cada extrínseca de cámara, puede agregar información de postura para dicha cámara. Para obtener más información, consulte Postura.

Matriz intrínseca

Ground Truth utiliza las matrices extrínsecas e intrínsecas de la cámara para calcular las métricas de visualización y transformar las etiquetas que van y salen de la escena 3D en imágenes de la cámara. Ground Truth calcula la matriz intrínseca de la cámara utilizando la distancia focal de la cámara (fx,fy) y las coordenadas del centro óptico (cx,cy) que proporcione. Para obtener más información, consulte Intrínseca y distorsión.

Distorsión de la imagen

La distorsión de la imagen puede ocurrir por diversas razones. Por ejemplo, las imágenes podrían distorsionarse debido a los efectos de barril o de ojo de pez. Ground Truth utiliza parámetros intrínsecos junto con un coeficiente de distorsión para anular la distorsión de las imágenes que proporciona al crear trabajos de etiquetado de nubes de puntos 3D. Si una imagen de cámara ya no está distorsionada, todos los coeficientes de distorsión deben establecerse en 0.

Para obtener más información acerca de las transformaciones que realiza Ground Truth para anular la distorsión de las imágenes, consulte Calibraciones de cámara: extrínseca, intrínseca y distorsión.

Vehículo ego

Para recopilar datos para aplicaciones de conducción autónomas, las mediciones utilizadas para generar datos de nubes de puntos se toman de sensores montados en un vehículo, o en el vehículo ego. Para proyectar ajustes de etiquetas que entran y salen de la escena 3D y las imágenes 2D, Ground Truth necesita que su vehículo ego se represente en un sistema de coordenadas universal. La postura del vehículo ego se compone de coordenadas de posición y cuaternión de orientación.

Ground Truth utiliza la postura del vehículo ego para calcular matrices de rotación y transformaciones. Las rotaciones en 3 dimensiones se pueden representar mediante una secuencia de 3 rotaciones alrededor de una secuencia de ejes. En teoría, tres ejes que abarcan el espacio euclidiano 3D son suficientes. En la práctica, los ejes de rotación se eligen para ser los vectores de base. Se espera que las tres rotaciones estén dentro de un fotograma de referencia global (extrínseco). Ground Truth no admite un fotograma de referencia centrado en el cuerpo (intrínseco), que está unido al objeto en rotación y se mueve con él. Para rastrear objetos, Ground Truth necesita medir desde una referencia global donde todos los vehículos se muevan. Cuando se utilizan trabajos de etiquetado de nubes de puntos 3D de Ground Truth, z especifica el eje de rotación (rotación extrínseca) y los ángulos de Euler de guiñada están en radianes (ángulo de rotación).

Postura

Ground Truth utiliza información de la postura para las visualizaciones 3D y la fusión de sensores. La información de postura que introduce a través de su archivo de manifiesto se utiliza para calcular matrices extrínsecas. Si ya tiene una matriz extrínseca, puede usarla para extraer datos de la postura del sensor y de la cámara.

Por ejemplo, en el conjunto de datos KITTI de conducción autónoma, el módulo python pykitti se puede utilizar para cargar los datos KITTI. En el conjunto de datos dataset.oxts[i].T_w_imu proporciona la transformación extrínseca LiDAR para el fotograma i^º y se puede multiplicar por los puntos para obtenerlos en un fotograma universal - matmul(lidar_transform_matrix, points). Esta transformación se puede convertir en posición (vector de traslación) y rumbo (en cuaternión) de LiDAR para el formato JSON del archivo de manifiesto de entrada. La transformación extrínseca de la cámara para cam0 en el fotograma i^º se puede calcular mediante inv(matmul(dataset.calib.T_cam0_velo, inv(dataset.oxts[i].T_w_imu))) y esto se puede convertir en rumbo y posición para cam0.


import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin= [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R

# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))

# heading in WCS using scipy 
heading = r.as_quat()
print(f"pose:{position}\nheading: {heading}")

Posición

En el archivo de manifiesto de entrada, position se refiere a la posición del sensor con respecto a un fotograma universal. Si no puede colocar la posición del dispositivo en un sistema de coordenadas universal, puede utilizar datos LiDAR con coordenadas locales. Del mismo modo, para cámaras de vídeo montadas puede especificar la posición y el rumbo en un sistema de coordenadas universal. Para la cámara, si no tiene información de posición, utilice (0, 0, 0).

Los siguientes son los campos del objeto de posición:

x (flotante): coordenada x de la posición del vehículo ego, el sensor o la cámara en metros.
y (flotante): coordenada y de la posición del vehículo ego, el sensor o la cámara en metros.
z (flotante): coordenada z de la posición del vehículo ego, el sensor o la cámara en metros.

A continuación se muestra un ejemplo de un objeto JSON position:


{
    "position": {
        "y": -152.77584902657554,
        "x": 311.21505956090624,
        "z": -10.854137529636024
      }
}

Heading

En el archivo de manifiesto de entrada, heading es un objeto que representa la orientación de un dispositivo con respecto al fotograma universal. Los valores de heading deben estar en cuaternión. Un cuaternión es una representación de la orientación consistente con las propiedades esféricas geodésicas. Si no puede poner el rumbo del sensor en coordenadas universales, utilice el cuaternión de identidad (qx = 0, qy = 0, qz = 0, qw = 1). Del mismo modo, en el caso de las cámaras, especifique el valor de heading en cuaterniones. Si no puede obtener parámetros de calibración de la cámara extrínseca, utilice también el cuaternión de identidad.

Los campos del objeto heading son los siguientes:

qx (flotante): componente x del vehículo ego, sensor u orientación de la cámara.
qy (flotante): componente y del vehículo ego, sensor u orientación de la cámara.
qz (flotante): componente z del vehículo ego, sensor u orientación de la cámara.
qw (flotante): w componente del vehículo ego, sensor u orientación de la cámara.

A continuación se muestra un ejemplo de un objeto JSON heading:


{
    "heading": {
        "qy": -0.7046155108831117,
        "qx": 0.034278837280808494,
        "qz": 0.7070617895701465,
        "qw": -0.04904659893885366
      }
}

Para obtener más información, consulte Cálculo de cuaterniones de orientación y posición.

Cálculo de cuaterniones de orientación y posición

Ground Truth requiere que todos los datos de orientación, o rumbo, se den en cuaterniones. Un cuaternión es una representación de la orientación consistente con las propiedades esféricas geodésicas que se pueden utilizar para aproximar la rotación. En comparación con los ángulos de Euler son más simples de componer y evitan el problema de bloqueo de cardán. En comparación con las matrices de rotación, son más compactos, más estables numéricamente y más eficientes.

Puede calcular cuaterniones a partir de una matriz de rotación o de una matriz de transformación.

Si tiene una matriz de rotación (compuesta por las rotaciones del eje) y un vector de traslación (u origen) en el sistema de coordenadas universal en lugar de una sola matriz de transformación rígida 4x4, puede utilizar directamente la matriz de rotación y el vector de traslación para calcular cuaterniones. Bibliotecas como scipy y pyqaternion pueden ayudar. El siguiente bloque de código muestra un ejemplo usando estas bibliotecas para calcular el cuaternion a partir de una matriz de rotación.


import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin = [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R
# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Una herramienta de interfaz de usuario como 3D Rotation Converter también puede resultar útil.

Si tiene una matriz de transformación extrínseca 4x4, tenga en cuenta que la matriz de transformación tiene el formato [R T; 0 0 0 1], donde R es la matriz de rotación y T es el vector de traslación de origen. Esto significa que puede extraer la matriz de rotación y el vector de traslación de la matriz de transformación de la siguiente manera.


import numpy as np

transformation 
= [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03, 1.71104606e+00],
   [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02, 5.80000039e-01],
   [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01, 9.43144935e-01],
   [              0,               0,               0,              1]]

transformation  = np.array(transformation )
rotation = transformation[0:3,0:3]
translation= transformation[0:3,3]

from scipy.spatial.transform import Rotation as R
# position is the origin translation
position = translation
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Con su propia configuración, puede calcular una matriz de transformación extrínseca utilizando la posición y orientación GPS/IMU (latitud, longitud, altitud y balanceo, paso, guiñada) con respecto al sensor LiDAR en el vehículo ego. Por ejemplo, puede calcular la postura a partir de datos sin procesar de KITTI utilizando pose = convertOxtsToPose(oxts) para transformar los datos de oxts en posturas euclidianas locales, especificadas por matrices de transformación rígidas 4x4. A continuación, puede transformar esta matriz de transformación de postura en un fotograma de referencia global utilizando la matriz de transformación de fotogramas de referencia en el sistema de coordenadas universal.


struct Quaternion
{
    double w, x, y, z;
};

Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
{
    // Abbreviations for the various angular functions
    double cy = cos(yaw * 0.5);
    double sy = sin(yaw * 0.5);
    double cp = cos(pitch * 0.5);
    double sp = sin(pitch * 0.5);
    double cr = cos(roll * 0.5);
    double sr = sin(roll * 0.5);

    Quaternion q;
    q.w = cr * cp * cy + sr * sp * sy;
    q.x = sr * cp * cy - cr * sp * sy;
    q.y = cr * sp * cy + sr * cp * sy;
    q.z = cr * cp * sy - sr * sp * cy;

    return q;
}

Transformaciones de fusión de sensores de Ground Truth

En las siguientes secciones, se profundiza en detalle en las transformaciones de la fusión de sensores de Ground Truth que se realizan utilizando los datos de postura que proporcione.

Extrínseca LiDAR

Para proyectar hacia y desde una escena 3D de LiDAR a la imagen 2D de una cámara, Ground Truth calcula las métricas de proyección de la transformación rígida utilizando la postura y el rumbo del vehículo ego. Ground Truth calcula la rotación y la traslación de las coordenadas de un mundo en el plano 3D mediante una secuencia simple de rotaciones y traslación.

Ground Truth calcula las métricas de rotación utilizando los cuaterniones de rumbo de la siguiente manera:

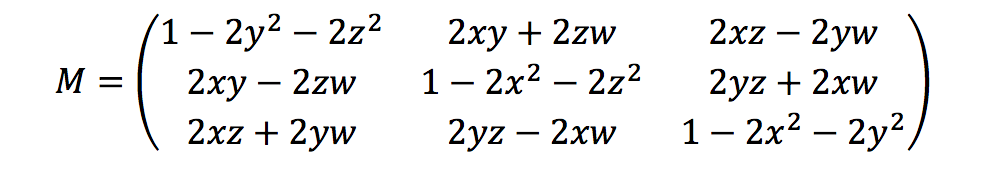
Ecuación: métricas de rotación de nubes de puntos de Ground Truth

Aquí, [x, y, z, w] corresponde a los parámetros del objeto JSON heading, [qx, qy, qz, qw]. Ground Truth calcula el vector de la columna de traslación como T = [poseX, poseY, poseZ]. Entonces las métricas extrínsecas son simplemente las siguientes:


LiDAR_extrinsic = [R T;0 0 0 1]

Calibraciones de cámara: extrínseca, intrínseca y distorsión

La calibración geométrica de la cámara, también conocida como reseccionamiento de cámara, calcula los parámetros de un objetivo y del sensor de imagen de una imagen o cámara de vídeo. Puede utilizar estos parámetros para corregir la distorsión del objetivo, medir el tamaño de un objeto en unidades universales o determinar la ubicación de la cámara en la escena. Los parámetros de la cámara incluyen coeficientes intrínsecos y de distorsión.

Extrínseca de cámara

Si se facilita la postura de la cámara, Ground Truth calcula la extrínseca de la cámara basándose en una transformación rígida del plano 3D al plano de la cámara. El cálculo es el mismo que el que se utiliza para Extrínseca LiDAR, salvo que Ground Truth utiliza la postura de la cámara (position y heading) y calcula la extrínseca inversa.


 camera_inverse_extrinsic = inv([Rc Tc;0 0 0 1]) #where Rc and Tc are camera pose components

Intrínseca y distorsión

Algunas cámaras, como las cámaras estenopeicas o de ojo de pez, pueden distorsionar de manera importante las fotografías. Esta distorsión se puede corregir mediante los coeficientes de distorsión y la distancia focal de la cámara. Para obtener más información, consulte Camera calibration With OpenCV en la documentación de OpenCV.

Hay dos tipos de distorsión que Ground Truth puede corregir: la distorsión radial y la distorsión tangencial.

La distorsión radial se produce cuando los rayos de luz se doblan más cerca de los bordes de una lente que en su centro óptico. Cuanto más pequeña sea la lente, mayor será la distorsión. La presencia de la distorsión radial se manifiesta en forma del efecto de barril u ojo de pez y Ground Truth utiliza la Fórmula 1 para anular la distorsión.

Fórmula 1:

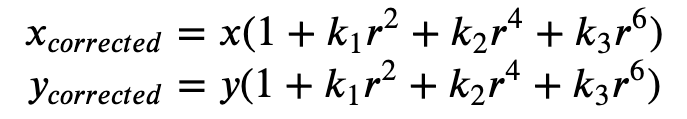
$Fórmula 1: ecuaciones para x_{corrected} e y_ {corrected}, para eliminar la distorsión de la distorsión radial$

La distorsión tangencial se produce porque las lentes utilizadas para tomar las imágenes no son perfectamente paralelas al plano de la imagen. Esto se puede corregir con la Fórmula 2.

Formula 2:

$Fórmula 2: ecuaciones para x_{corrected} e y_{corrected}, para corregir la distorsión tangencial$

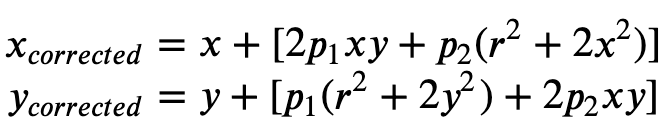
En el archivo de manifiesto de entrada, puede proporcionar coeficientes de distorsión para que Ground Truth anule la distorsión de las imágenes. Todos los coeficientes de distorsión son flotantes.

k1, k2, k3, k4: coeficientes de distorsión radial. Utilizados para modelos de cámara de ojo de pez y estenopeicas.
p1 ,p2: coeficientes de distorsión tangencial. Utilizados para modelos de cámara estenopeicas.

Si las imágenes ya no están distorsionadas, todos los coeficientes de distorsión deben ser 0 en el manifiesto de entrada.

Con el fin de reconstruir correctamente la imagen corregida, Ground Truth hace una conversión de unidad de las imágenes basada en longitudes focales. Si se usa una distancia focal común con una relación de aspecto dada para ambos ejes, como 1, en la fórmula superior tendremos una distancia focal única. La matriz que contiene estos cuatro parámetros se conoce como la matriz de calibración intrínseca en cámara.

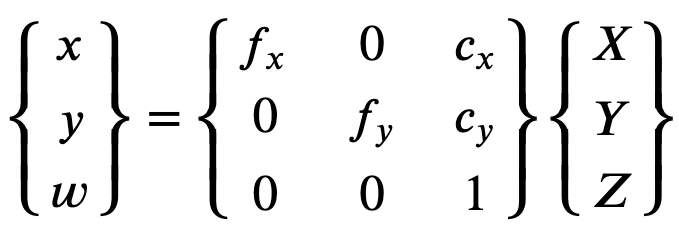
Matriz de calibración intrínseca de la cámara

Aunque los coeficientes de distorsión son los mismos independientemente de las resoluciones de la cámara utilizadas, estos deben escalarse con la resolución actual de la resolución calibrada.

Los siguientes son valores flotantes.

fx: distancia focal en dirección x.
fy: distancia focal en dirección y.
cx: coordenada x del punto principal.
cy: coordenada y del punto principal.

Ground Truth utiliza la extrínseca de la cámara y la intrínseca de la cámara para calcular las métricas de visualización, tal y como se muestra en el siguiente bloque de código para transformar etiquetas entre la escena 3D y las imágenes 2D.


def generate_view_matrix(intrinsic_matrix, extrinsic_matrix):
    intrinsic_matrix = np.c_[intrinsic_matrix, np.zeros(3)]
    view_matrix = np.matmul(intrinsic_matrix, extrinsic_matrix)
    view_matrix = np.insert(view_matrix, 2, np.array((0, 0, 0, 1)), 0)
    return view_matrix

Aviso JavaScript está desactivado o no está disponible en su navegador.

Para utilizar la documentación de AWS, debe estar habilitado JavaScript. Para obtener más información, consulte las páginas de ayuda de su navegador.

Convenciones del documento

Crear un manifiesto de entrada de secuencia de nube de puntos

Datos de entrada de fotogramas de vídeo