Les traductions sont fournies par des outils de traduction automatique. En cas de conflit entre le contenu d'une traduction et celui de la version originale en anglais, la version anglaise prévaudra.

Bonjour AHS : Exécutez votre première simulation hamiltonienne analogique

Cette section fournit des informations sur l'exécution de votre première simulation hamiltonienne analogique.

Chaîne de spin en interaction

Pour un exemple canonique d'un système de nombreuses particules en interaction, considérons un anneau de huit spins (dont chacun peut être dans les états « haut » ↑ ⟩ et « bas »). Bien que petit, ce système modèle présente déjà une poignée de phénomènes intéressants liés aux matériaux magnétiques naturels. Dans cet exemple, nous allons montrer comment préparer un ordre dit antiferromagnétique, dans lequel des spins consécutifs pointent dans des directions opposées.

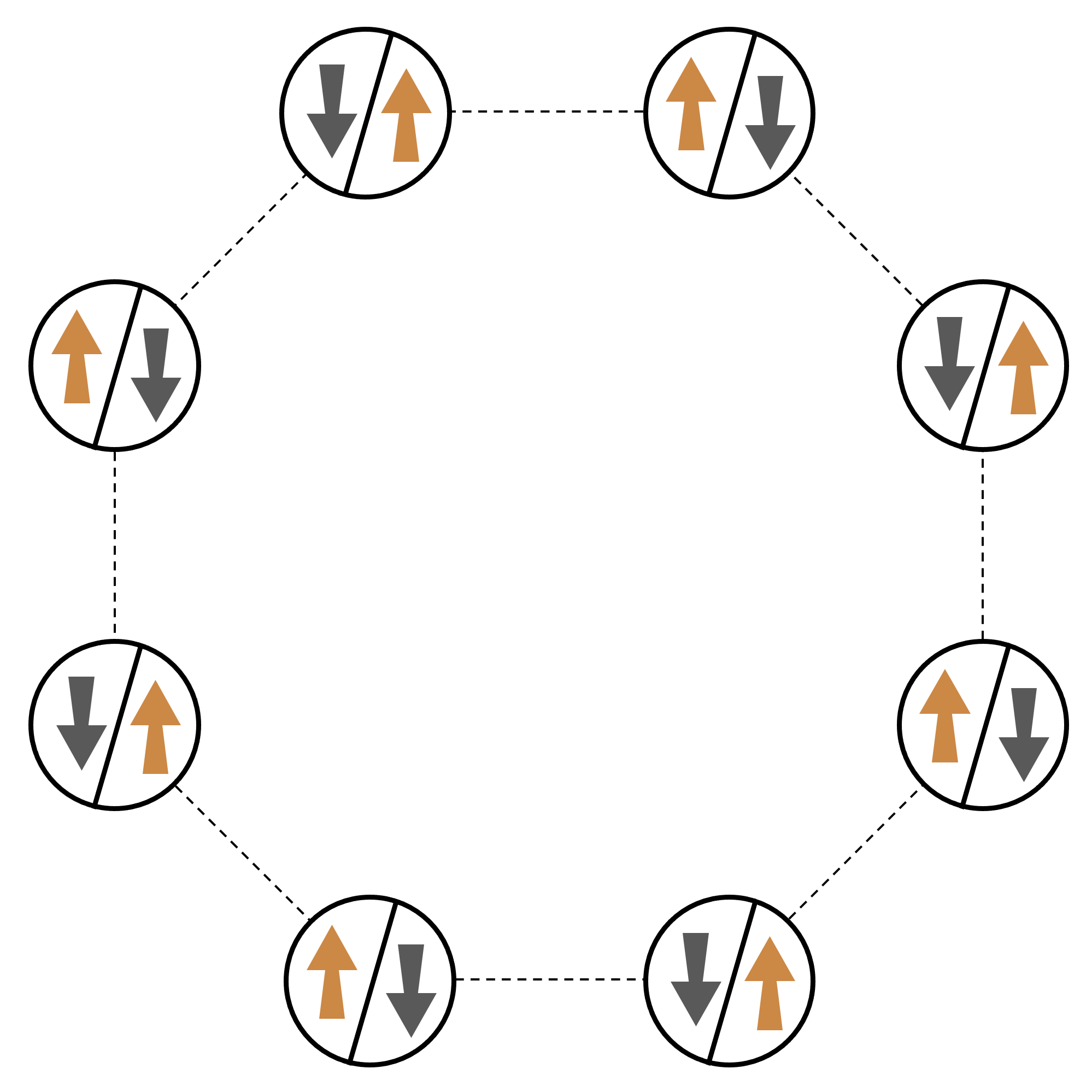
Arrangement

Nous utiliserons un atome neutre pour représenter chaque spin, et les états de spin « haut » et « bas » seront codés dans l'état de Rydberg excité et dans l'état fondamental des atomes, respectivement. Tout d'abord, nous créons l'arrangement 2D. Nous pouvons programmer l'anneau de tours ci-dessus avec le code suivant.

Prérequis : Vous devez installer le support par pip. SDK (Si vous utilisez une instance de bloc-notes hébergée par Braket, celle-ci SDK est préinstallée avec les blocs-notes.) Pour reproduire les tracés, vous devez également installer matplotlib séparément à l'aide de la commande shell. pip install matplotlib

import numpy as np
   import matplotlib.pyplot as plt  # required for plotting
   
   from braket.ahs.atom_arrangement import AtomArrangement
   
   a = 5.7e-6  # nearest-neighbor separation (in meters)
   
   register = AtomArrangement()
   register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

avec lequel nous pouvons également comploter

fig, ax = plt.subplots(1, 1, figsize=(7,7))
   xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
   ax.plot(xs, ys, 'r.', ms=15)
   for idx, (x, y) in enumerate(zip(xs, ys)):
       ax.text(x, y, f" {idx}", fontsize=12)
   plt.show()  # this will show the plot below in an ipython or jupyter session

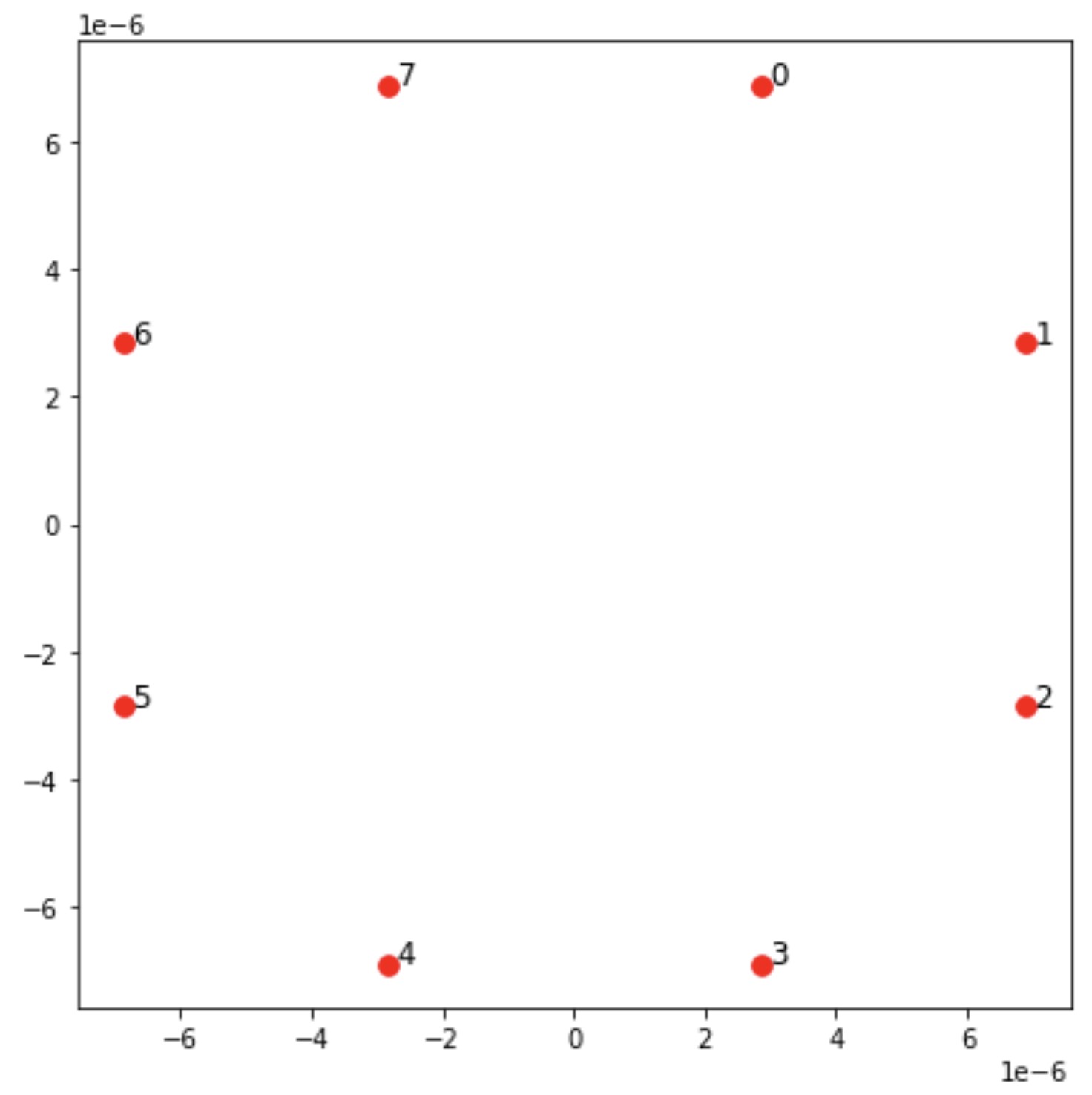
Interaction

Pour préparer la phase antiferromagnétique, nous devons induire des interactions entre des spins voisins. Pour cela, nous utilisons l'interaction de van der Waals, qui est implémentée nativement par des appareils à atomes neutres (tels que le Aquila appareil de QuEra). En utilisant la représentation du spin, le terme hamiltonien pour cette interaction peut être exprimé sous la forme d'une somme de toutes les paires de spins (j, k).

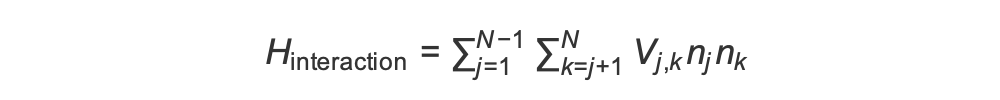
Ici, nj=↑ _j ⟨↑ est _j un opérateur qui prend la valeur 1 uniquement si le spin j est à l'état « up », et 0 dans le cas contraire. La force est V _j,k =C₆/(d_j,k​) ⁶, où C ₆ est le coefficient fixe, et d _j,k est la distance euclidienne entre les spins j et k. L'effet immédiat de ce terme d'interaction est que tout état dans lequel le spin j et le spin k sont à la fois « en hausse » produit une énergie élevée (de la quantité V_j,k). En concevant soigneusement le reste du AHS programme, cette interaction empêchera les spins voisins d'être tous deux à l'état « actif », un effet communément appelé « blocus de Rydberg ».

Champ de conduite

Au début du AHS programme, tous les spins (par défaut) démarrent dans leur état « down », ils sont dans une phase dite ferromagnétique. En gardant un œil sur notre objectif de préparer la phase antiferromagnétique, nous avons spécifié un champ de commande cohérent dépendant du temps qui fait passer en douceur les spins de cet état à un état à plusieurs corps où les états « haut » sont préférés. L'hamiltonien correspondant peut être écrit comme

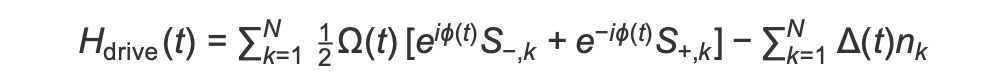
où Ω (t), φ (t), Δ (t) sont l'amplitude globale (ou fréquence de Rabi), la phase et le désaccord du champ moteur en fonction du temps, affectant tous les spins de manière uniforme. Ici_−,k, S _+,k =↓ _k​ ⟨↑ _k et S =( S_−,k) ^† _k​ =↑ _{k k k k} La partie Ω du champ moteur couple de manière cohérente les états « bas » et « haut » de tous les spins simultanément, tandis que la partie Δ contrôle la récompense énergétique pour les états « haut ».

Pour programmer une transition en douceur de la phase ferromagnétique à la phase antiferromagnétique, nous indiquons le champ de commande avec le code suivant.

from braket.timings.time_series import TimeSeries
   from braket.ahs.driving_field import DrivingField
   
   # smooth transition from "down" to "up" state
   time_max = 4e-6  # seconds
   time_ramp = 1e-7  # seconds
   omega_max = 6300000.0  # rad / sec
   delta_start = -5 * omega_max
   delta_end = 5 * omega_max
   
   omega = TimeSeries()
   omega.put(0.0, 0.0)
   omega.put(time_ramp, omega_max)
   omega.put(time_max - time_ramp, omega_max)
   omega.put(time_max, 0.0)
   
   delta = TimeSeries()
   delta.put(0.0, delta_start)
   delta.put(time_ramp, delta_start)
   delta.put(time_max - time_ramp, delta_end)
   delta.put(time_max, delta_end)
   
   phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)
   
   drive = DrivingField(
       amplitude=omega,
       phase=phi,
       detuning=delta
   )

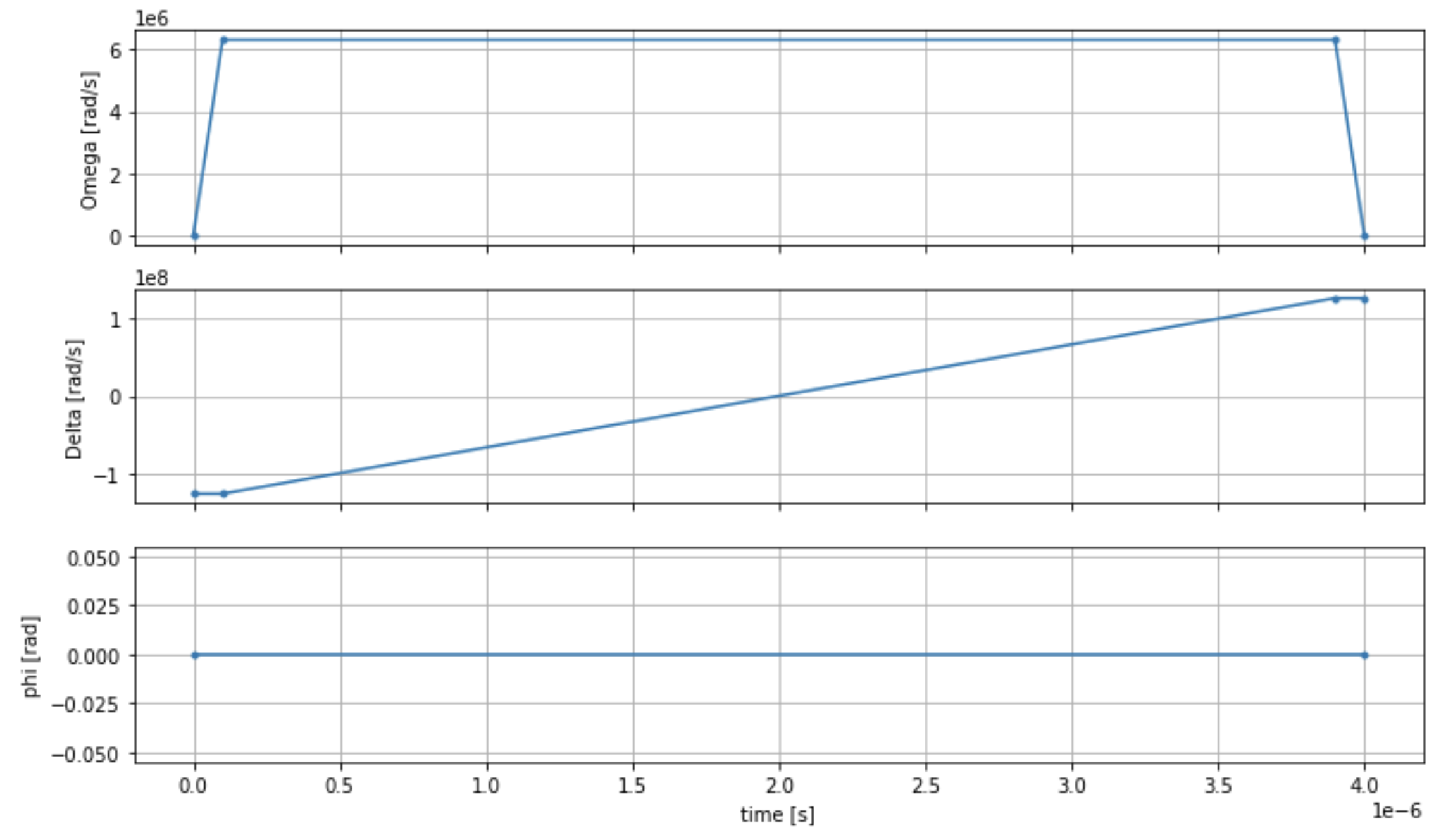
Nous pouvons visualiser les séries chronologiques du champ de conduite avec le script suivant.

fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)
   
   ax = axes[0]
   time_series = drive.amplitude.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Omega [rad/s]')
   
   ax = axes[1]
   time_series = drive.detuning.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Delta [rad/s]')
   
   ax = axes[2]
   time_series = drive.phase.time_series
   # Note: time series of phase is understood as a piecewise constant function
   ax.step(time_series.times(), time_series.values(), '.-', where='post');
   ax.set_ylabel('phi [rad]')
   ax.grid()
   ax.set_xlabel('time [s]')
   
   plt.show()  # this will show the plot below in an ipython or jupyter session

AHSprogramme

Le registre, le champ de conduite (et les interactions implicites de van der Waals) constituent le programme de simulation hamiltonienne analogique. ahs_program

from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation
   
   ahs_program = AnalogHamiltonianSimulation(
       register=register,
       hamiltonian=drive
   )

Exécution sur un simulateur local

Comme cet exemple est petit (moins de 15 tours), avant de l'exécuter sur un AHS -compatibleQPU, nous pouvons l'exécuter sur le AHS simulateur local fourni avec le SDK Braket. Le simulateur local étant disponible gratuitement avec le BraketSDK, il s'agit d'une bonne pratique pour garantir que notre code puisse s'exécuter correctement.

Ici, nous pouvons régler le nombre de prises à une valeur élevée (disons, 1 million) car le simulateur local suit l'évolution temporelle de l'état quantique et prélève des échantillons à partir de l'état final, augmentant ainsi le nombre de prises de vue, tout en n'augmentant que légèrement le temps d'exécution total.

from braket.devices import LocalSimulator
   device = LocalSimulator("braket_ahs")
   
   result_simulator = device.run(
       ahs_program,
       shots=1_000_000
   ).result()  # takes about 5 seconds

Analyse des résultats du simulateur

Nous pouvons agréger les résultats des tirs à l'aide de la fonction suivante qui déduit l'état de chaque rotation (qui peut être « d » pour « vers le bas », « u » pour « haut » ou « e » pour un site vide) et compte le nombre de fois où chaque configuration s'est produite sur les plans.

from collections import Counter
   
   def get_counts(result):
       """Aggregate state counts from AHS shot results
   
       A count of strings (of length = # of spins) are returned, where
       each character denotes the state of a spin (site):
          e: empty site
          u: up state spin
          d: down state spin
   
       Args:
          result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)
   
       Returns
           dict: number of times each state configuration is measured
   
       """
       state_counts = Counter()
       states = ['e', 'u', 'd']
       for shot in result.measurements:
           pre = shot.pre_sequence
           post = shot.post_sequence
           state_idx = np.array(pre) * (1 + np.array(post))
           state = "".join(map(lambda s_idx: states[s_idx], state_idx))
           state_counts.update((state,))
       return dict(state_counts)
   
   counts_simulator = get_counts(result_simulator)  # takes about 5 seconds
   print(counts_simulator)

{'udududud': 330944, 'dudududu': 329576, 'dududdud': 38033, ...}

countsVoici un dictionnaire qui compte le nombre de fois où chaque configuration d'état est observée sur les plans. Nous pouvons également les visualiser avec le code suivant.

from collections import Counter
   
   def has_neighboring_up_states(state):
       if 'uu' in state:
           return True
       if state[0] == 'u' and state[-1] == 'u':
           return True
       return False
   
   def number_of_up_states(state):
       return Counter(state)['u']
   
   def plot_counts(counts):
       non_blockaded = []
       blockaded = []
       for state, count in counts.items():
           if not has_neighboring_up_states(state):
               collection = non_blockaded
           else:
               collection = blockaded
           collection.append((state, count, number_of_up_states(state)))
   
       blockaded.sort(key=lambda _: _[1], reverse=True)
       non_blockaded.sort(key=lambda _: _[1], reverse=True)
   
       for configurations, name in zip((non_blockaded,
                                       blockaded),
                                       ('no neighboring "up" states',
                                       'some neighboring "up" states')):
           plt.figure(figsize=(14, 3))
           plt.bar(range(len(configurations)), [item[1] for item in configurations])
           plt.xticks(range(len(configurations)))
           plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
           plt.ylabel('shots')
           plt.grid(axis='y')
           plt.title(f'{name} configurations')
           plt.show()
   
   plot_counts(counts_simulator)

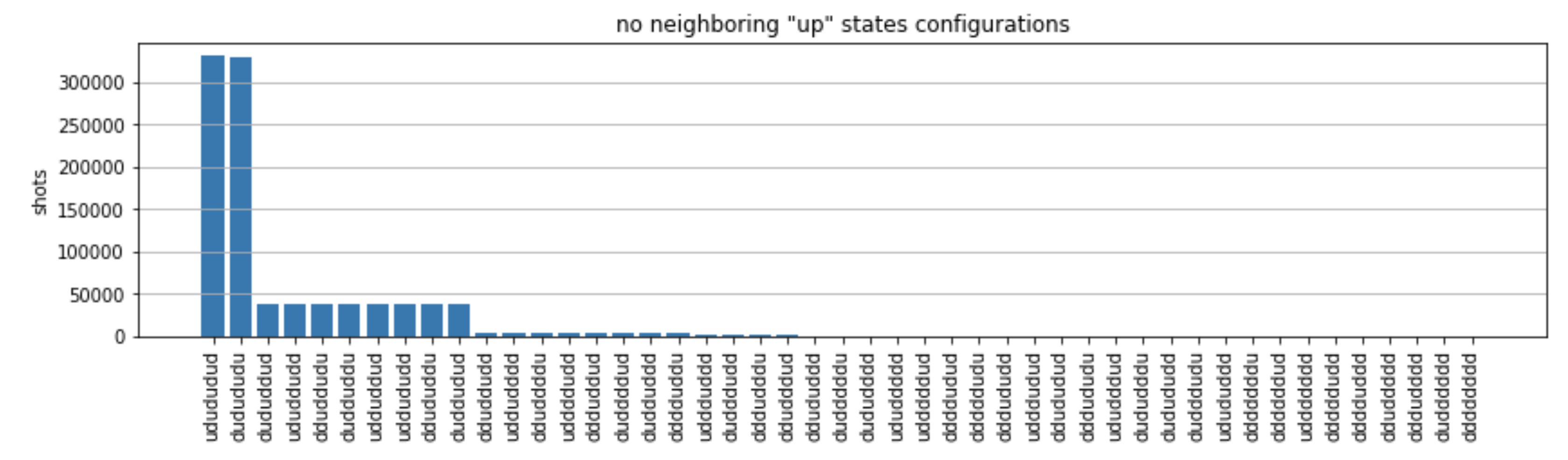
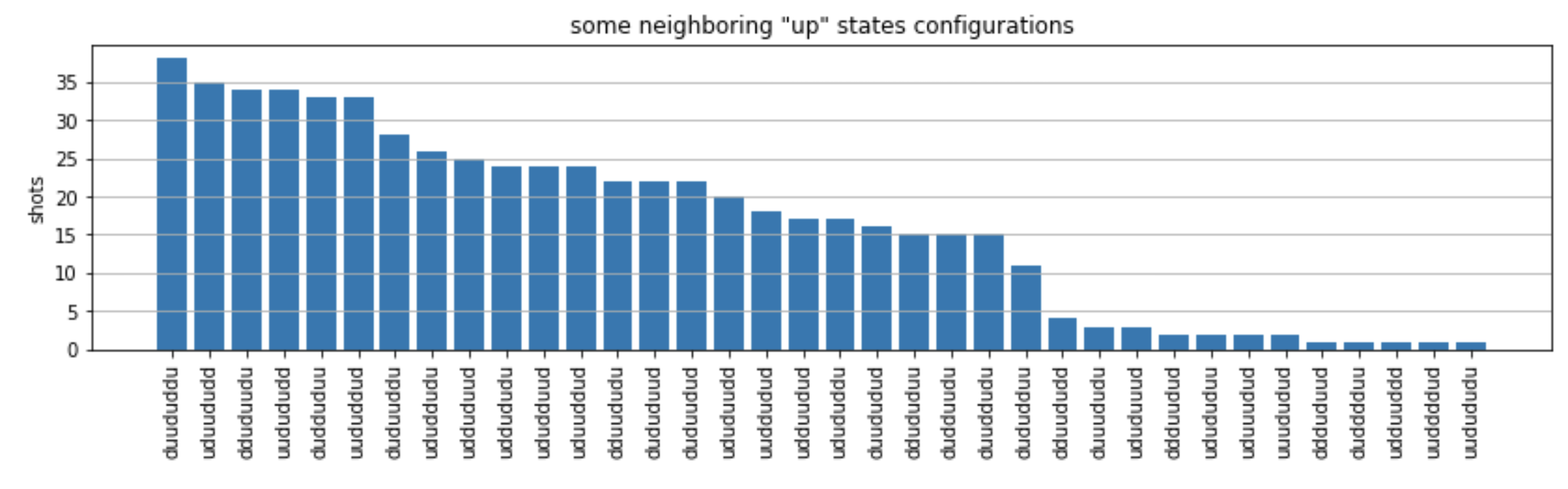
À partir des graphiques, nous pouvons lire les observations suivantes pour vérifier que nous avons bien préparé la phase antiferromagnétique.

Running on QuEra's Aquila QPU

Conditions préalables : Outre l'installation du Braket par pip SDK, si vous utilisez Amazon Braket pour la première fois, assurez-vous d'avoir suivi les étapes de démarrage nécessaires.

Une fois toutes les dépendances installées, nous pouvons nous connecter au Aquila QPU.

from braket.aws import AwsDevice
   
   aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

Pour adapter notre AHS programme aux QuEra machine, nous devons arrondir toutes les valeurs pour respecter les niveaux de précision autorisés par le Aquila QPU. (Ces exigences sont régies par les paramètres de l'appareil dont le nom contient « Résolution ». Nous pouvons les voir en les exécutant aquila_qpu.properties.dict() dans un carnet. Pour plus de détails sur les fonctionnalités et les exigences d'Aquila, consultez le bloc-notes Introduction à Aquila.) Nous pouvons le faire en appelant la discretize méthode.

discretized_ahs_program = ahs_program.discretize(aquila_qpu)

Nous pouvons maintenant exécuter le programme (en exécutant seulement 100 prises pour le moment) sur le Aquila QPU.

task = aquila_qpu.run(discretized_ahs_program, shots=100)
   
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")

task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: CREATED

En raison de la grande variation de la durée d'exécution d'une tâche quantique (en fonction des fenêtres de disponibilité et de QPU l'utilisation), il est conseillé de noter la tâche ARN quantique afin que nous puissions vérifier son statut ultérieurement à l'aide de l'extrait de code suivant.

# Optionally, in a new python session
   
   from braket.aws import AwsQuantumTask
   
   SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"
   
   task = AwsQuantumTask(arn=SAVED_TASK_ARN)
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")

*[Output]*
   task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: COMPLETED

Une fois le statut atteint COMPLETED (qui peut également être vérifié depuis la page des tâches quantiques de la console Amazon Braket), nous pouvons interroger les résultats avec :

result_aquila = task.result()

Analyse des QPU résultats

En utilisant les mêmes get_counts fonctions que précédemment, nous pouvons calculer les nombres :

counts_aquila = get_counts(result_aquila)
   print(counts_aquila)

*[Output]*
   {'udududud': 24, 'dudududu': 17, 'dududdud': 3, ...}

et tracez-les avec plot_counts :

plot_counts(counts_aquila)

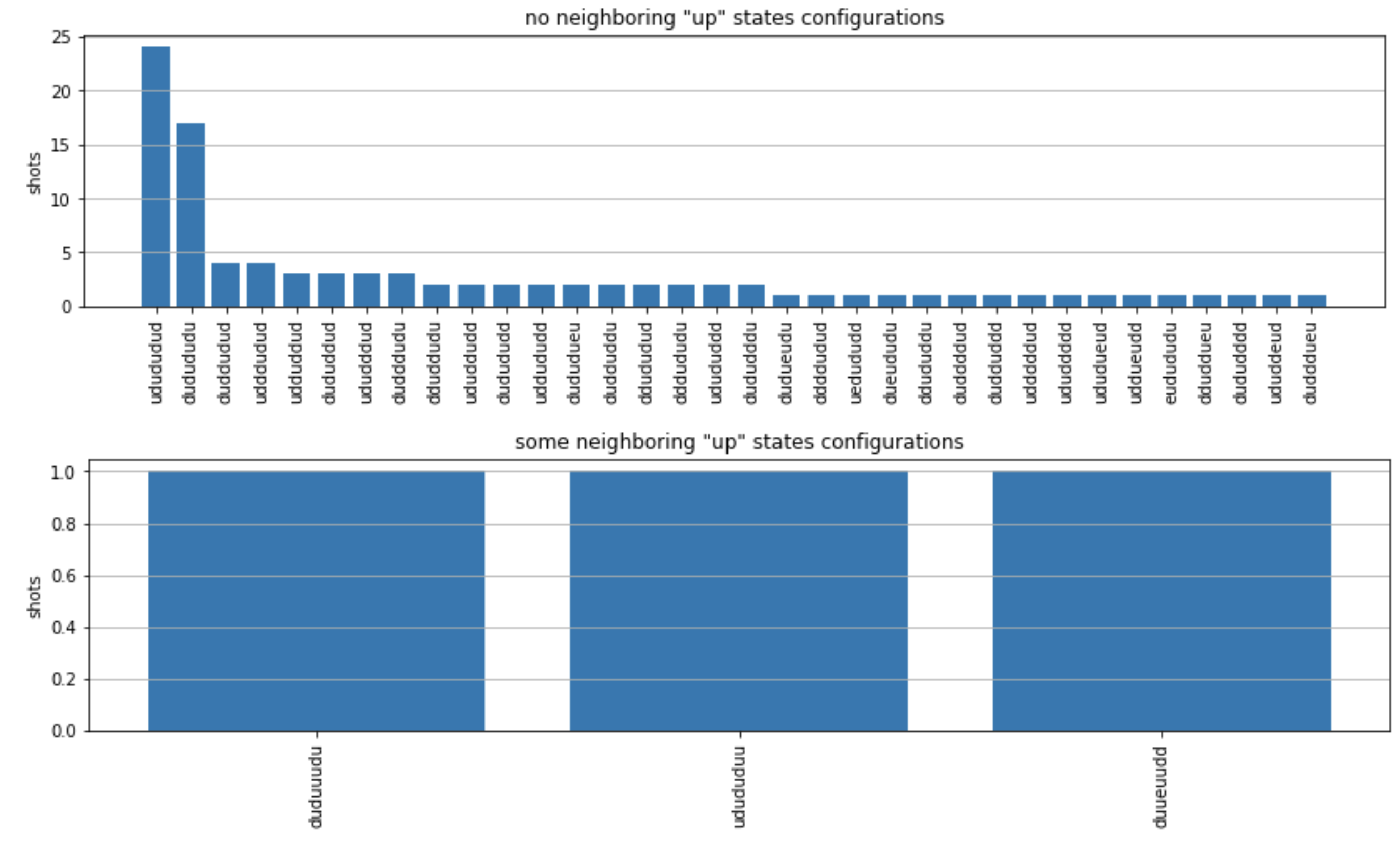
Notez qu'une petite partie des plans comportent des sites vides (marqués d'un « e »). Cela est dû à des imperfections de préparation de 1 à 2 % par atome du Aquila QPU. En outre, les résultats correspondent à la simulation dans les limites des fluctuations statistiques attendues en raison du faible nombre de prises de vue.

Étapes suivantes

Félicitations, vous venez d'exécuter votre première AHS charge de travail sur Amazon Braket à l'aide du AHS simulateur local et du Aquila QPU.

Pour en savoir plus sur la physique de Rydberg, la simulation hamiltonienne analogique et Aquila appareil, reportez-vous à nos exemples de blocs-notes.