Fonctionnement du parallélisme de tenseur - Amazon SageMaker
Comment la bibliothèque adapte le parallélisme des tenseurs au module PyTorch nn.Linear

Les traductions sont fournies par des outils de traduction automatique. En cas de conflit entre le contenu d'une traduction et celui de la version originale en anglais, la version anglaise prévaudra.

Fonctionnement du parallélisme de tenseur

Le parallélisme de tenseur a lieu au niveau des nn.Modules ; il partitionne des modules spécifiques du modèle sur des rangs parallèles au tenseur. Cela se produit en plus de la partition existante de l'ensemble de modules utilisé dans le parallélisme de pipeline.

Lorsqu'un module est partitionné au moyen d'un parallélisme de tenseur, sa propagation vers l'avant et l'arrière est distribuée. La bibliothèque gère la communication nécessaire entre les appareils pour implémenter l'exécution distribuée de ces modules. Les modules sont partitionnés sur plusieurs rangs parallèles de données. Contrairement à la distribution classique des charges de travail, les rangs parallèles aux données ne possèdent pas le réplica complet du modèle lorsque le parallélisme de tenseur de la bibliothèque est utilisé. Au lieu de cela, chaque rang parallèle aux données peut comporter uniquement une partition des modules distribués, en plus de l'intégralité des modules qui ne sont pas distribués.

Exemple : imaginez un parallélisme de tenseur entre des rangs parallèles aux données, où le degré de parallélisme de données est de 4 et le degré de parallélisme de tenseur est de 2. Supposons que vous disposez d'un groupe parallèle aux données qui contient l'arborescence de modules suivante, après avoir partitionné l'ensemble de modules.

A
├── B
|   ├── E
|   ├── F
├── C
└── D
    ├── G
    └── H

Supposons que le parallélisme de tenseur soit pris en charge pour les modules B, G et H. L'un des résultats possibles de la partition parallèle au tenseur de ce modèle pourrait être :

dp_rank 0 (tensor parallel rank 0): A, B:0, C, D, G:0, H
dp_rank 1 (tensor parallel rank 1): A, B:1, C, D, G:1, H
dp_rank 2 (tensor parallel rank 0): A, B:0, C, D, G:0, H
dp_rank 3 (tensor parallel rank 1): A, B:1, C, D, G:1, H

Chaque ligne représente l'ensemble des modules stockés dans ce dp_rank et la notation X:y représente la y-ième fraction du module X. Notez ce qui suit :

  1. Le partitionnement a lieu entre des sous-ensembles de rangs parallèles aux données, que nous appelons TP_GROUP, et non pas dans l'intégralité du DP_GROUP. Dès lors, la partition du modèle exacte est répliquée sur dp_rank 0 et dp_rank 2, et de la même manière sur dp_rank 1 et dp_rank 3.

  2. Les modules E et F ne font plus partie du modèle, car leur module parent B est partitionné et toute exécution qui fait normalement partie des modules E et F se déroule au sein du module B (partitionné).

  3. Même si le module H est pris en charge pour le parallélisme de tenseur, dans cet exemple, il n'est pas partitionné, ce qui souligne que le partitionnement d'un module dépend de l'entrée utilisateur. Le fait qu'un module soit pris en charge pour le parallélisme de tenseur ne signifie pas nécessairement qu'il est partitionné.

Comment la bibliothèque adapte le parallélisme des tenseurs au module PyTorch nn.Linear

Lorsque le parallélisme de tenseur est effectué sur des rangs parallèles aux données, un sous-ensemble des paramètres, des gradients et des états de l'optimiseur est partitionné entre les dispositifs parallèles au tenseur pour les modules partitionnés. Pour le reste des modules, les dispositifs parallèles au tenseur fonctionnent de manière parallèle aux données classique. Pour exécuter le module partitionné, un appareil collecte d'abord les parties nécessaires de tous les échantillons de données sur des appareils homologues dans le même groupe de parallélisme de tenseur. L'appareil exécute ensuite la fraction locale du module sur tous ces échantillons de données, suivie d'un autre cycle de synchronisation qui combine les parties de la sortie pour chaque échantillon de données et renvoie les échantillons de données combinés à l'origine GPUs de l'échantillon de données. La figure suivante montre un exemple de ce processus sur un module nn.Linear partitionné.

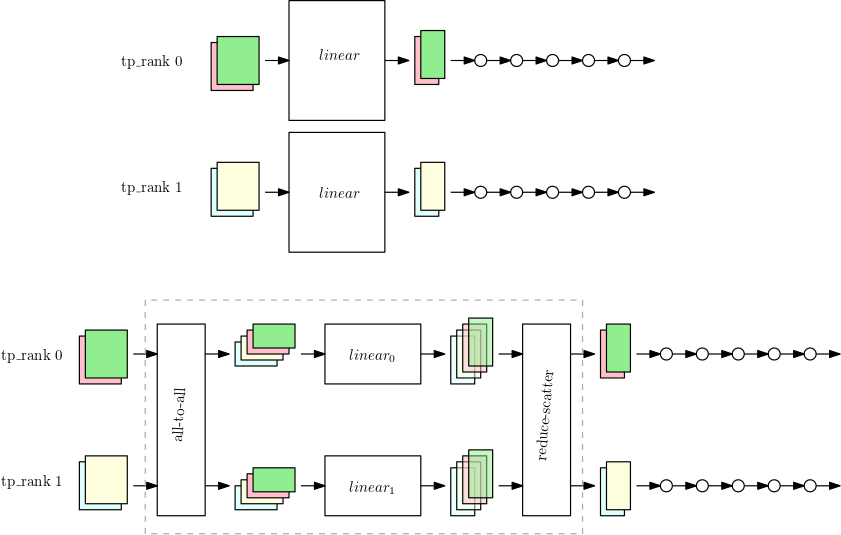
Deux figures illustrant deux concepts de tensor parallel.

La première figure montre un petit modèle présentant un grand module nn.Linear avec parallélisme de données sur les deux rangs de parallélisme de tenseur. Le module nn.Linear est répliqué dans les deux rangs parallèles.

La deuxième figure montre le parallélisme de tenseurs appliqué sur un modèle plus grand lors du fractionnement du module nn.Linear. Chaque tp_rank contient la moitié du module linéaire et la totalité du reste des opérations. Pendant l'exécution du module linéaire, chaque tp_rank collecte la moitié pertinente de tous les échantillons de données et la transmet par leur moitié du module nn.Linear. Le résultat doit être réduit et dispersé (avec sommation comme opération de réduction) afin que chaque rang ait la sortie linéaire finale de ses propres échantillons de données. Le reste du modèle s'exécute de manière parallèle aux données classique.