Les traductions sont fournies par des outils de traduction automatique. En cas de conflit entre le contenu d'une traduction et celui de la version originale en anglais, la version anglaise prévaudra.

Comprendre les systèmes de coordonnées et la fusion de capteurs

Les données de nuage de points sont toujours situées dans un système de coordonnées. Ce système de coordonnées peut être local au véhicule ou à l'appareil captant les environs, ou il peut s'agir d'un système de coordonnées mondial. Lorsque vous utilisez des tâches d'étiquetage de nuage de points 3D Ground Truth, toutes les annotations sont générées à l'aide du système de coordonnées de vos données source. Pour certains types de tâches et fonctions d'étiquetage, vous devez fournir les données dans un système de coordonnées mondial.

Dans cette rubrique, vous allez apprendre ce qui suit :

Configuration requise pour le système de coordonnées utilisé pour les tâches d'étiquetage

Si vos données de nuage de points ont été collectées dans un système de coordonnées local, vous pouvez utiliser une matrice extrinsèque du capteur utilisé pour collecter les données pour les convertir en un système de coordonnées mondial ou en un système de référence mondial. Si vous ne pouvez pas obtenir de métriques extrinsèques pour vos données de nuage de points et que, par conséquent, vous ne pouvez pas obtenir de nuages de points dans un système de coordonnées mondial, vous pouvez fournir des données de nuage de points dans un système de coordonnées local pour les types de tâches de détection d'objets de nuage de points 3D et de segmentation sémantique de nuage de points 3D.

Pour le suivi d'objets, vous devez fournir les données de nuage de points dans un système de coordonnées mondial. En effet, lorsque vous suivez des objets à travers plusieurs trames, le véhicule ego lui-même se déplace dans le monde et donc toutes les trames ont besoin d'un point de référence.

Si vous incluez des données de caméra pour la fusion des capteurs, il est recommandé de fournir des poses de caméra dans le même système de coordonnées mondial que le capteur 3D (tel qu'un capteur LiDAR).

Utilisation de données de nuage de points dans un système de coordonnées mondial

Cette section explique ce qu'est un système de coordonnées mondial (WCS), également appelé système de référence mondial, et explique comment fournir des données de nuage de points dans un système de coordonnées mondial.

Qu'est-ce qu'un système de coordonnées mondial (WCS) ?

Un WCS ou système de référence mondial est un système de coordonnées universel fixe dans lequel les systèmes de coordonnées du véhicule et du capteur sont placés. Par exemple, si plusieurs trames de nuages de points sont situés dans des systèmes de coordonnées différents parce qu'ils ont été collectés à partir de deux capteurs, un WCS peut être utilisé pour convertir toutes les coordonnées dans ces trames de nuages de points en un seul système de coordonnées, où toutes les trames ont la même origine (0,0,0). Cette transformation s'effectue en convertissant l'origine de chaque trame en l'origine du WCS à l'aide d'un vecteur de translation, et en faisant pivoter les trois axes (généralement x, y et z) dans la bonne direction à l'aide d'une matrice de rotation. Cette transformation du corps rigide est appelée transformation homogène.

Un système de coordonnées mondiales est important dans la planification globale des chemins, la localisation, le mappage et les simulations de scénarios de conduite. Ground Truth utilise le système de coordonnées mondiales cartésiennes orienté main droite tel que celui défini dans la norme ISO 8855, où l'axe x est orienté vers l'avant, vers le mouvement de la voiture, l'axe y est orienté vers la gauche et l'axe z pointe vers le haut à partir du sol.

Le système de référence mondial dépend des données. Certains jeux de données utilisent la position LiDAR dans la première trame comme origine. Dans ce scénario, toutes les trames utilisent la première trame comme référence, et le cap et la position de l'appareil seront proches de l'origine dans la première trame. Par exemple, les ensembles de données KITTI utilisent la première trame comme référence pour les coordonnées mondiales. D'autres jeux de données utilisent une position d'appareil différente de celle l'origine.

Notez qu'il ne s'agit pas du système de GPS/IMU coordinate system, which is typically rotated by 90 degrees along the z-axis. If your point cloud data is in a GPS/IMU coordonnées (comme les OXT dans le jeu de données open source AV KITTI). Vous devez alors transformer l'origine en un système de coordonnées mondial (généralement le système de coordonnées de référence du véhicule). Vous appliquez cette transformation en multipliant vos données par des métriques de transformation (matrice de rotation et vecteur de translation). Cela permet de transformer les données du système de coordonnées d'origine en un système de coordonnées de référence mondial. Pour de plus amples informations sur cette transformation, veuillez consulter la section suivante.

Convertir des données de nuage de points 3D en un WCS

Ground Truth suppose que vos données de nuage de points ont déjà été transformées en un système de coordonnées de référence de votre choix. Par exemple, vous pouvez choisir le système de coordonnées de référence du capteur (tel que LiDAR) comme système de coordonnées de référence mondial. Vous pouvez également prendre des nuages de points provenant de différents capteurs et les transformer d'une vue du capteur en une vue du système de coordonnées de référence du véhicule. Vous utilisez la matrice extrinsèque d'un capteur, composée d'une matrice de rotation et d'un vecteur de translation, pour convertir vos données de nuage de points en un système de référence WCS ou mondial.

Collectivement, le vecteur de translation et la matrice de rotation peuvent être utilisés pour constituer une matrice extrinsèque, qui peut être utilisée pour convertir des données d'un système de coordonnées local en un système WCS. Par exemple, votre matrice extrinsèque LiDAR peut être composée comme suit, où R est la matrice de rotation et T, le vecteur de translation :

LiDAR_extrinsic = [R T;0 0 0 1]

Par exemple, l'ensemble de données KITTI de conduite autonome inclut une matrice de rotation et un vecteur de translation pour la matrice de transformation extrinsèque LiDAR pour chaque trame. Le module python pykitti peut être utilisé pour charger les données KITTI, et dans l'ensemble de données, dataset.oxts[i].T_w_imu donne la transformation extrinsèque LiDAR pour la i^ème trame qui peut être multipliée par des points de cette trame pour les convertir en un système mondial - np.matmul(lidar_transform_matrix, points). La multiplication d'un point dans une trame LiDAR par une matrice extrinsèque LiDAR le transforme en coordonnées mondiales. La multiplication d'un point du système mondial par la matrice extrinsèque de la caméra donne les coordonnées du point dans le système de référence de la caméra.

L'exemple de code suivant montre comment convertir des trames de nuages de points de l'ensemble de données KITTI en un système WCS.

import pykitti
import numpy as np

basedir = '/Users/nameofuser/kitti-data'
date = '2011_09_26'
drive = '0079'

# The 'frames' argument is optional - default: None, which loads the whole dataset.
# Calibration, timestamps, and IMU data are read automatically. 
# Camera and velodyne data are available via properties that create generators
# when accessed, or through getter methods that provide random access.
data = pykitti.raw(basedir, date, drive, frames=range(0, 50, 5))

# i is frame number
i = 0

# lidar extrinsic for the ith frame
lidar_extrinsic_matrix = data.oxts[i].T_w_imu

# velodyne raw point cloud in lidar scanners own coordinate system
points = data.get_velo(i)

# transform points from lidar to global frame using lidar_extrinsic_matrix
def generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix):
    tps = []
    for point in points:
        transformed_points = np.matmul(lidar_extrinsic_matrix, np.array([point[0], point[1], point[2], 1], dtype=np.float32).reshape(4,1)).tolist()
        if len(point) > 3 and point[3] is not None:
            tps.append([transformed_points[0][0], transformed_points[1][0], transformed_points[2][0], point[3]])
       
    return tps
    
# customer transforms points from lidar to global frame using lidar_extrinsic_matrix
transformed_pcl = generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix)    

Fusion de capteurs

Ground Truth prend en charge la fusion de capteurs de données de nuage de points avec un maximum de 8 entrées de caméra vidéo. Cette fonctionnalité permet aux étiqueteurs humains de visualiser l'image du nuage de points 3D side-by-side avec l'image vidéo synchronisée. En plus de fournir davantage de contexte visuel pour l'étiquetage, la fusion des capteurs permet aux collaborateurs d'ajuster les annotations dans la scène 3D et dans les images 2D, et le réglage est projeté dans l'autre vue. La vidéo suivante illustre une tâche d'étiquetage de nuage de points 3D avec le système LiDAR et la fusion de capteurs de caméra.

Pour obtenir de meilleurs résultats, lorsque vous utilisez la fusion de capteurs, votre nuage de points doit se trouver dans un WCS. Ground Truth utilise les informations de pose de votre capteur (comme LiDAR), de votre caméra et de votre véhicule ego pour calculer des matrices extrinsèques et intrinsèques pour la fusion des capteurs.

Matrice extrinsèque

Ground Truth utilise des matrices extrinsèques et intrinsèques de caméra, et des matrices extrinsèques de capteur (comme LiDAR) pour projeter des objets vers et depuis la trame de référence des données de nuage de points en direction de la trame de référence de la caméra.

Par exemple, pour projeter une étiquette du nuage de points 3D vers le plan d'image de la caméra, Ground Truth transforme les points 3D du système de coordonnées de LiDAR en système de coordonnées de la caméra. Cela se fait généralement en transformant d'abord des points 3D du système de coordonnées propre à LiDAR en un système de coordonnées mondial (ou un système de référence global) à l'aide de la matrice extrinsèque LiDAR. Ground Truth utilise ensuite l'extrinsèque inverse de la caméra (qui convertit les points d'une image de référence globale en la trame de référence de la caméra) pour transformer les points 3D du système de coordonnées mondial obtenu à l'étape précédente dans le plan d'image de la caméra. La matrice extrinsèque LiDAR peut également être utilisée pour transformer des données 3D en un système de coordonnées mondial. Si vos données 3D sont déjà transformées en système de coordonnées mondial, la première transformation n'a aucun impact sur la translation des étiquettes, et la translation des étiquettes dépend uniquement de la matrice extrinsèque inverse de la caméra. Une matrice d'affichage est utilisée pour visualiser les étiquettes projetées. Pour de plus amples informations sur ces transformations et sur la matrice d'affichage, veuillez consulter Transformations de fusion des capteurs de Ground Truth.

Ground Truth calcule ces matrices extrinsèques à l'aide des données de pose LiDAR et des données de pose de la caméra que vous fournissez : heading (en quaternions : qx, qy, qz et qw) et position (x, y, z). Pour le véhicule, le cap et la position sont généralement décrits dans la trame de référence du véhicule dans un système de coordonnées mondial et sont appelés pose du véhicule ego. Pour chaque matrice extrinsèque de la caméra, vous pouvez ajouter des informations de pose associées à cette caméra. Pour de plus amples informations, veuillez consulter Expression.

Matrice intrinsèque

Ground Truth utilise les matrices extrinsèques et intrinsèques de la caméra pour calculer les métriques de vue afin de transformer les étiquettes vers et depuis la scène 3D en images de la caméra. Ground Truth calcule la matrice intrinsèque de la caméra à l'aide de la distance focale de la caméra (fx, fy) et les coordonnées du centre optique (cx, cy) que vous fournissez. Pour de plus amples informations, veuillez consulter Métriques intrinsèques et distorsion.

Distorsion de l'image

Une distorsion de l'image peut se produire pour diverses raisons. Par exemple, les images peuvent être déformées en raison d'effets de tonneau ou d'oeil de poisson. Ground Truth utilise des paramètres intrinsèques, ainsi que des coefficients de distorsion, pour supprimer la déformation des images que vous fournissez lors de la création de tâches d'étiquetage de nuage de points 3D. Si la déformation d'une image de caméra a déjà été corrigée, tous les coefficients de distorsion doivent être réglés sur 0.

Pour en savoir plus sur les transformations effectuées par Ground Truth pour supprimer les déformations des images, veuillez consulter Calibrations de caméra : extrinsèque, intrinsèque et distorsion.

Véhicule ego

Pour collecter des données pour les applications de conduite autonome, les mesures utilisées pour générer des données de nuage de points sont récupérées à partir de capteurs montés sur un véhicule, le véhicule ego. Pour projeter des ajustements d'étiquette sur et à partir de la scène 3D et des images 2D, Ground Truth a besoin des données de pose de votre véhicule ego dans un système de coordonnées mondial. Les données de pose du véhicule ego sont composées des coordonnées de position et du quaternion d'orientation.

Ground Truth utilise les données de pose de votre véhicule ego pour calculer les matrices de rotation et de transformation. Les rotations en 3 dimensions peuvent être représentées par une séquence de 3 rotations autour d'une séquence d'axes. En théorie, trois axes couvrant l'espace euclidien 3D suffisent. En pratique, les axes de rotation sont choisis comme vecteurs de base. Les trois rotations devraient se situer dans un cadre de référence global (extrinsèque). Ground Truth n'est pas un cadre de référence centré sur le corps de support (intrinsèque) qui est attaché à l'objet en rotation et se déplace avec celui-ci. Pour suivre les objets, Ground Truth doit effectuer les mesures à partir d'un système de référence mondial où tous les véhicules se déplacent. Lorsque vous utilisez des tâches d'étiquetage de nuage de points 3D Ground Truth, z spécifie l'axe de rotation (rotation extrinsèque) et les angles d'Euler en lacet sont exprimés en radians (angle de rotation).

Expression

Ground Truth utilise les informations de pose pour les visualisations 3D et la fusion de capteurs. Les informations de pose que vous saisissez via votre fichier manifeste sont utilisées pour calculer des matrices extrinsèques. Si vous disposez déjà d'une matrice extrinsèque, vous pouvez l'utiliser pour extraire les données de pose du capteur et de la caméra.

Par exemple, dans l'ensemble de données KITTI de conduite autonome, le module python pykitti peut être utilisé pour charger les données KITTI. Dans l'ensemble de données, dataset.oxts[i].T_w_imu fournit la transformation extrinsèque LiDAR pour la i^ème trame et il peut être multiplié par les points pour les obtenir dans un système mondial - matmul(lidar_transform_matrix, points). Cette transformation peut être convertie en position (vecteur de translation) et en cap (en quaternion) de LiDAR pour le format JSON du fichier manifeste d'entrée. La transformation extrinsèque de la caméra pour cam0 dans la i^ème trame peut être calculée via inv(matmul(dataset.calib.T_cam0_velo, inv(dataset.oxts[i].T_w_imu))) et ce résultat peut être converti en données de cap et de position pour cam0.

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin= [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R

# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))

# heading in WCS using scipy 
heading = r.as_quat()
print(f"pose:{position}\nheading: {heading}")

Position

Dans le fichier manifeste d'entrée, position fait référence à la position du capteur par rapport à un système mondial. Si vous ne parvenez pas à exprimer la position de l'appareil dans un système de coordonnées mondial, vous pouvez utiliser des données LiDAR avec des coordonnées locales. De même, pour les caméras vidéo montées, vous pouvez spécifier la position et le cap dans un système de coordonnées mondial. Pour la caméra, si vous n'avez pas d'informations de position, veuillez utiliser (0, 0, 0).

Voici les champs de l'objet de position :

Voici un exemple d'objet JSON position :

{
    "position": {
        "y": -152.77584902657554,
        "x": 311.21505956090624,
        "z": -10.854137529636024
      }
}

Titre

Dans le fichier manifeste d'entrée, heading est un objet qui représente l'orientation d'un appareil par rapport au système mondial. Les valeurs de cap doivent être en quaternion. Un quaternion est une représentation de l'orientation compatible avec les propriétés des sphères géodésiques. Si vous ne parvenez pas à exprimer le cap du capteur en coordonnées mondiales, veuillez utiliser le quaternion d'identité (qx = 0, qy = 0, qz = 0, qw = 1). De même, pour les caméras, spécifiez le cap en quaternions. Si vous ne parvenez pas à obtenir les paramètres de calibration extrinsèques de la caméra, veuillez également utiliser le quaternion d'identité.

Les champs présents dans l'objet heading sont les suivants :

Voici un exemple d'objet JSON heading :

{
    "heading": {
        "qy": -0.7046155108831117,
        "qx": 0.034278837280808494,
        "qz": 0.7070617895701465,
        "qw": -0.04904659893885366
      }
}

Pour en savoir plus, consultez Calcul des quaternions d'orientation et de la position.

Calcul des quaternions d'orientation et de la position

Ground Truth exige que toutes les données d'orientation, ou de cap, soient données en quaternions. Un quaternion est une représentation de l'orientation compatible avec les propriétés des sphères géodésiques qui peut être utilisée pour faire une estimation de la rotation. Par rapport aux angles d'Euler, les quaternions sont plus simples à composer et évitent le problème du blocage de cardan. Comparés aux matrices de rotation, ils sont plus compacts, plus stables numériquement et plus efficaces.

Vous pouvez calculer des quaternions à partir d'une matrice de rotation ou d'une matrice de transformation.

Si vous avez une matrice de rotation (composée des rotations d'axes) et un vecteur de translation (ou origine) dans le système de coordonnées mondial au lieu d'une seule matrice de transformation rigide 4x4, vous pouvez utiliser directement la matrice de rotation et le vecteur de translation pour calculer les quaternions. Des bibliothèques telles que scipy et pyqaternion peuvent vous aider. Le bloc de code suivant montre un exemple utilisant ces bibliothèques pour calculer le quaternion à partir d'une matrice de rotation.

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin = [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R
# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Un outil d'interface utilisateur tel que 3D Rotation Converter peut également être utile.

Si vous avez une matrice de transformation extrinsèque 4x4, notez que la matrice de transformation se présente sous la forme [R T; 0 0 0 1], où R est la matrice de rotation et T, le vecteur de translation d'origine. Cela signifie que vous pouvez extraire la matrice de rotation et le vecteur de translation de la matrice de transformation comme suit.

import numpy as np

transformation 
= [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03, 1.71104606e+00],
   [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02, 5.80000039e-01],
   [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01, 9.43144935e-01],
   [              0,               0,               0,              1]]

transformation  = np.array(transformation )
rotation = transformation[0:3,0:3]
translation= transformation[0:3,3]

from scipy.spatial.transform import Rotation as R
# position is the origin translation
position = translation
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Avec votre propre configuration, vous pouvez calculer une matrice de transformation extrinsèque en utilisant la position et l'orientation GPS/IMU (latitude, longitude, altitude et roulis, tangage, lacet) par rapport au capteur LiDAR sur le véhicule ego. Par exemple, vous pouvez calculer les données de pose à partir de données brutes KITTI en utilisant pose = convertOxtsToPose(oxts) pour transformer les données oxts en poses euclidiennes locales, spécifiées par des matrices de transformation rigides 4x4. Vous pouvez ensuite transformer cette matrice de transformation de données de pose en système de référence mondial à l'aide de la matrice de transformation des trames de référence dans le système de coordonnées mondial.

struct Quaternion
{
    double w, x, y, z;
};

Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
{
    // Abbreviations for the various angular functions
    double cy = cos(yaw * 0.5);
    double sy = sin(yaw * 0.5);
    double cp = cos(pitch * 0.5);
    double sp = sin(pitch * 0.5);
    double cr = cos(roll * 0.5);
    double sr = sin(roll * 0.5);

    Quaternion q;
    q.w = cr * cp * cy + sr * sp * sy;
    q.x = sr * cp * cy - cr * sp * sy;
    q.y = cr * sp * cy + sr * cp * sy;
    q.z = cr * cp * sy - sr * sp * cy;

    return q;
}

Transformations de fusion des capteurs de Ground Truth

Les sections suivantes expliquent plus en détail les transformations de fusion des capteurs Ground Truth effectuées à l'aide des données de pose que vous fournissez.

Métriques extrinsèques LiDAR

Afin d'effectuer une projection vers et depuis une scène LiDAR 3D vers une image de caméra 2D, Ground Truth calcule les métriques de projection de transformation rigides à l'aide des données de pose et de cap du véhicule ego. Ground Truth calcule la rotation et la translation des coordonnées mondiales dans le plan 3D en effectuant une simple séquence de rotations et de translation.

Ground Truth calcule les métriques de rotation à l'aide des quaternions de cap comme suit :

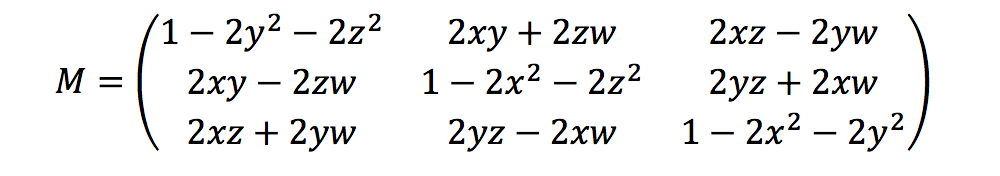
Ici, [x, y, z, w] correspond aux paramètres dans l'objet JSON heading, soit [qx, qy, qz, qw]. Ground Truth calcule le vecteur de colonne de traduction en tant que T = [poseX, poseY, poseZ]. Ensuite, les métriques extrinsèques sont simplement les suivantes :

LiDAR_extrinsic = [R T;0 0 0 1]

Calibrations de caméra : extrinsèque, intrinsèque et distorsion

La calibration géométrique de la caméra, également appelée camera resectioning, évalue les paramètres d'un objectif et d'un capteur d'image ou d'une image ou une vidéo prise par la caméra. Vous pouvez utiliser ces paramètres pour corriger la distorsion de l'objectif, mesurer la taille d'un objet en unités mondiales ou déterminer l'emplacement de la caméra dans la scène. Les paramètres de caméra incluent les coefficients intrinsèques et de distorsion.

Métriques extrinsèques de la caméra

Si les données de pose de la caméra sont fournies, Ground Truth calcule les métriques extrinsèques de la caméra en fonction d'une transformation rigide du plan 3D en plan de la caméra. Le calcul est le même que celui utilisé pour les Métriques extrinsèques LiDAR, sauf que Ground Truth utilise les données de pose de la caméra (position et heading) et calcule les métriques extrinsèques inverses.

 camera_inverse_extrinsic = inv([Rc Tc;0 0 0 1]) #where Rc and Tc are camera pose components

Métriques intrinsèques et distorsion

Certains appareils photo, tels que les appareils photo sténopé ou fisheye, peuvent introduire une distorsion importante dans les photos. Cette distorsion peut être corrigée à l'aide de coefficients de distorsion et de la distance focale de la caméra. Pour en savoir plus, veuillez consulter Étalonnage de la caméra avec OpenCV dans la documentation OpenCV.

Il existe deux types de distorsion que Ground Truth peut corriger : la distorsion radiale et la distorsion tangentielle.

La distorsion radiale se produit lorsque les rayons lumineux se courbent plus près des bords d'un objectif qu'ils ne le font à son centre optique. Plus l'objectif est petit, plus la distorsion est grande. La présence de la distorsion radiale se manifeste sous la forme de l'effet de tonneau ou fish-eye et Ground Truth utilise Formula 1 pour la supprimer.

Formule 1 :

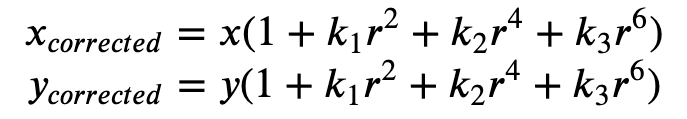
La distorsion tangentielle se produit parce que les objectifs utilisés pour prendre les images ne sont pas parfaitement parallèles au plan des images. Cela peut être corrigé avec la Formule 2.

Formule 2 :

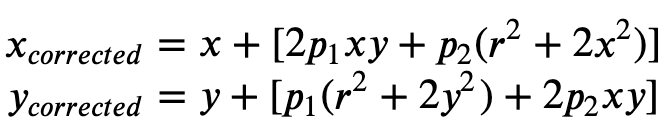
Dans le fichier manifeste source, vous pouvez fournir des coefficients de distorsion et Ground Truth supprimera la distorsion de vos images. Tous les coefficients de distorsion sont des valeurs flottantes.

Si la déformation des images a déjà été supprimée, tous les coefficients de distorsion doivent être 0 dans votre manifeste d'entrée.

Afin de reconstruire correctement l'image corrigée, Ground Truth effectue une conversion d'unité des images basée sur les distances focales. Si une distance focale courante est utilisée avec un rapport de forme donné pour les deux axes, tel que 1, dans la formule supérieure, nous aurons une distance focale unique. La matrice contenant ces quatre paramètres est appelée matrice de calibration intrinsèque en caméra.

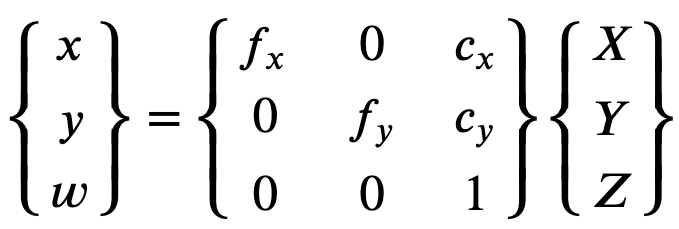
Bien que les coefficients de distorsion soient les mêmes quelles que soient les résolutions utilisées pour la caméra, ceux-ci doivent être mis à l'échelle avec la résolution actuelle provenant de la résolution calibrée.

Les valeurs suivantes sont des valeurs flottantes.

Ground Truth utilise les métriques extrinsèques et les métriques intrinsèques de la caméra pour calculer les mesures d'affichage, comme indiqué dans le bloc de code suivant pour transformer les étiquettes entre la scène 3D et les images 2D.

def generate_view_matrix(intrinsic_matrix, extrinsic_matrix):
    intrinsic_matrix = np.c_[intrinsic_matrix, np.zeros(3)]
    view_matrix = np.matmul(intrinsic_matrix, extrinsic_matrix)
    view_matrix = np.insert(view_matrix, 2, np.array((0, 0, 0, 1)), 0)
    return view_matrix