Memahami Sistem Koordinat dan Sensor Fusion - Amazon SageMaker
Persyaratan Sistem Koordinat untuk Pekerjaan PelabelanMenggunakan Point Cloud Data dalam Sistem Koordinat DuniaSensor FusionKuarter dan Posisi Orientasi HitungTransformasi Fusi Sensor Ground Truth

Terjemahan disediakan oleh mesin penerjemah. Jika konten terjemahan yang diberikan bertentangan dengan versi bahasa Inggris aslinya, utamakan versi bahasa Inggris.

Memahami Sistem Koordinat dan Sensor Fusion

Data awan titik selalu terletak di sistem koordinat. Sistem koordinat ini mungkin lokal untuk kendaraan atau perangkat yang merasakan lingkungan, atau mungkin sistem koordinat dunia. Saat Anda menggunakan pekerjaan pelabelan cloud titik 3D Ground Truth, semua anotasi dibuat menggunakan sistem koordinat data input Anda. Untuk beberapa jenis dan fitur tugas pekerjaan pelabelan, Anda harus memberikan data dalam sistem koordinat dunia.

Dalam topik ini, Anda akan mempelajari hal berikut:

  • Ketika Anda diminta untuk memberikan data input dalam sistem koordinat dunia atau kerangka acuan global.

  • Apa itu koordinat dunia dan bagaimana Anda dapat mengonversi data cloud titik ke sistem koordinat dunia.

  • Bagaimana Anda dapat menggunakan sensor dan matriks ekstrinsik kamera untuk memberikan data pose saat menggunakan fusi sensor.

Persyaratan Sistem Koordinat untuk Pekerjaan Pelabelan

Jika data cloud titik Anda dikumpulkan dalam sistem koordinat lokal, Anda dapat menggunakan matriks ekstrinsik dari sensor yang digunakan untuk mengumpulkan data untuk mengubahnya menjadi sistem koordinat dunia atau kerangka acuan global. Jika Anda tidak dapat memperoleh ekstrinsik untuk data cloud titik Anda dan, sebagai hasilnya, tidak dapat memperoleh awan titik dalam sistem koordinat dunia, Anda dapat memberikan data cloud titik dalam sistem koordinat lokal untuk deteksi objek cloud titik 3D dan jenis tugas segmentasi semantik.

Untuk pelacakan objek, Anda harus menyediakan data cloud titik dalam sistem koordinat dunia. Ini karena ketika Anda melacak objek di beberapa bingkai, kendaraan ego itu sendiri bergerak di dunia sehingga semua bingkai membutuhkan titik referensi.

Jika Anda menyertakan data kamera untuk fusi sensor, disarankan agar Anda memberikan pose kamera dalam sistem koordinat dunia yang sama dengan sensor 3D (seperti DAR sensor Li).

Menggunakan Point Cloud Data dalam Sistem Koordinat Dunia

Bagian ini menjelaskan apa itu sistem koordinat dunia (WCS), juga disebut sebagai kerangka acuan global, dan menjelaskan bagaimana Anda dapat menyediakan data cloud titik dalam sistem koordinat dunia.

Apa itu Sistem Koordinat Dunia?

Kerangka acuan global WCS atau global adalah sistem koordinat universal tetap di mana sistem koordinat kendaraan dan sensor ditempatkan. Misalnya, jika beberapa bingkai awan titik terletak di sistem koordinat yang berbeda karena dikumpulkan dari dua sensor, a WCS dapat digunakan untuk menerjemahkan semua koordinat dalam kerangka awan titik ini ke dalam satu sistem koordinat, di mana semua bingkai memiliki asal yang sama, (0,0,0). Transformasi ini dilakukan dengan menerjemahkan asal setiap frame ke asal WCS menggunakan vektor translasi, dan memutar tiga sumbu (biasanya x, y, dan z) ke orientasi yang tepat menggunakan matriks rotasi. Transformasi tubuh kaku ini disebut transformasi homogen.

Sistem koordinat dunia penting dalam perencanaan jalur global, lokalisasi, pemetaan, dan simulasi skenario mengemudi. Ground Truth menggunakan sistem koordinat dunia Cartesian tangan kanan seperti yang didefinisikan pada ISO8855, di mana sumbu x maju menuju gerakan mobil, sumbu y kiri, dan sumbu z mengarah ke atas dari tanah.

Kerangka acuan global tergantung pada data. Beberapa dataset menggunakan DAR posisi Li di frame pertama sebagai asal. Dalam skenario ini, semua frame menggunakan frame pertama sebagai referensi dan heading dan posisi perangkat akan berada di dekat asal di frame pertama. Misalnya, KITTI kumpulan data memiliki kerangka pertama sebagai referensi untuk koordinat dunia. Kumpulan data lain menggunakan posisi perangkat yang berbeda dari asalnya.

Perhatikan bahwa ini bukan sistem IMU koordinatGPS/, yang biasanya diputar 90 derajat di sepanjang sumbu z. Jika data cloud titik Anda berada dalam sistem IMU koordinatGPS/(seperti OXTs di KITTI kumpulan data AV open source), maka Anda perlu mengubah asal menjadi sistem koordinat dunia (biasanya sistem koordinat referensi kendaraan). Anda menerapkan transformasi ini dengan mengalikan data Anda dengan metrik transformasi (matriks rotasi dan vektor terjemahan). Ini akan mengubah data dari sistem koordinat aslinya menjadi sistem koordinat referensi global. Pelajari lebih lanjut tentang transformasi ini di bagian selanjutnya.

Mengkonversi 3D Point Cloud Data ke a WCS

Ground Truth mengasumsikan bahwa data cloud titik Anda telah diubah menjadi sistem koordinat referensi pilihan Anda. Misalnya, Anda dapat memilih sistem koordinat referensi sensor (seperti LiDAR) sebagai sistem koordinat referensi global Anda. Anda juga dapat mengambil awan titik dari berbagai sensor dan mengubahnya dari tampilan sensor ke tampilan sistem koordinat referensi kendaraan. Anda menggunakan matriks ekstrinsik sensor, yang terdiri dari matriks rotasi dan vektor terjemahan, untuk mengonversi data awan titik Anda ke kerangka acuan global WCS atau global.

Secara kolektif, vektor translasi dan matriks rotasi dapat digunakan untuk membuat matriks ekstrinsik, yang dapat digunakan untuk mengubah data dari sistem koordinat lokal ke a. WCS Misalnya, matriks DAR ekstrinsik Li Anda dapat disusun sebagai berikut, di mana R matriks rotasi dan T merupakan vektor terjemahan:

LiDAR_extrinsic = [R T;0 0 0 1]

Misalnya, KITTI dataset mengemudi otonom mencakup matriks rotasi dan vektor translasi untuk matriks transformasi DAR ekstrinsik Li untuk setiap frame. Modul pykitti python dapat digunakan untuk memuat KITTI data, dan dalam kumpulan data dataset.oxts[i].T_w_imu memberikan transformasi DAR ekstrinsik Li untuk frame i th dengan dapat dikalikan dengan titik-titik dalam bingkai itu untuk mengubahnya menjadi kerangka dunia -. np.matmul(lidar_transform_matrix, points) Mengalikan titik dalam DAR bingkai Li dengan matriks DAR ekstrinsik Li mengubahnya menjadi koordinat dunia. Mengalikan titik dalam bingkai dunia dengan matriks ekstrinsik kamera memberikan koordinat titik dalam kerangka acuan kamera.

Contoh kode berikut menunjukkan bagaimana Anda dapat mengonversi frame awan titik dari KITTI kumpulan data menjadi file. WCS 

import pykitti
import numpy as np

basedir = '/Users/nameofuser/kitti-data'
date = '2011_09_26'
drive = '0079'

# The 'frames' argument is optional - default: None, which loads the whole dataset.
# Calibration, timestamps, and IMU data are read automatically. 
# Camera and velodyne data are available via properties that create generators
# when accessed, or through getter methods that provide random access.
data = pykitti.raw(basedir, date, drive, frames=range(0, 50, 5))

# i is frame number
i = 0

# lidar extrinsic for the ith frame
lidar_extrinsic_matrix = data.oxts[i].T_w_imu

# velodyne raw point cloud in lidar scanners own coordinate system
points = data.get_velo(i)

# transform points from lidar to global frame using lidar_extrinsic_matrix
def generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix):
    tps = []
    for point in points:
        transformed_points = np.matmul(lidar_extrinsic_matrix, np.array([point[0], point[1], point[2], 1], dtype=np.float32).reshape(4,1)).tolist()
        if len(point) > 3 and point[3] is not None:
            tps.append([transformed_points[0][0], transformed_points[1][0], transformed_points[2][0], point[3]])
       
    return tps
    
# customer transforms points from lidar to global frame using lidar_extrinsic_matrix
transformed_pcl = generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix)

Sensor Fusion

Ground Truth mendukung fusi sensor data titik cloud dengan hingga 8 input kamera video. Fitur ini memungkinkan pelabel manusia untuk melihat bingkai awan titik 3D side-by-side dengan bingkai video yang disinkronkan. Selain menyediakan lebih banyak konteks visual untuk pelabelan, fusi sensor memungkinkan pekerja untuk menyesuaikan anotasi dalam adegan 3D dan dalam gambar 2D dan penyesuaian diproyeksikan ke tampilan lain. Video berikut menunjukkan pekerjaan pelabelan awan titik 3D dengan Li DAR dan fusi sensor kamera.

Gif menunjukkan pekerjaan pelabelan awan titik 3D dengan Li DAR dan fusi sensor kamera.

Untuk hasil terbaik, saat menggunakan fusi sensor, awan titik Anda harus berada di aWCS. Ground Truth menggunakan sensor Anda (seperti LiDAR), kamera, dan informasi pose kendaraan ego untuk menghitung matriks ekstrinsik dan intrinsik untuk fusi sensor.

Matriks Ekstrinsik

Ground Truth menggunakan sensor (seperti LiDAR) ekstrinsik dan matriks ekstrinsik dan intrinsik kamera untuk memproyeksikan objek ke dan dari kerangka acuan data cloud titik ke kerangka acuan kamera.

Misalnya, untuk memproyeksikan label dari cloud titik 3D ke bidang gambar kamera, Ground Truth mengubah titik 3D dari sistem koordinat DAR Li sendiri ke sistem koordinat kamera. Ini biasanya dilakukan dengan terlebih dahulu mengubah titik 3D dari sistem koordinat DAR Li sendiri ke sistem koordinat dunia (atau kerangka referensi global) menggunakan matriks DAR ekstrinsik Li. Ground Truth kemudian menggunakan kamera inverse ekstrinsik (yang mengubah titik dari kerangka acuan global ke kerangka acuan kamera) untuk mengubah titik-titik 3D dari sistem koordinat dunia yang diperoleh pada langkah sebelumnya menjadi bidang gambar kamera. Matriks DAR ekstrinsik Li juga dapat digunakan untuk mengubah data 3D menjadi sistem koordinat dunia. Jika data 3D Anda sudah diubah menjadi sistem koordinat dunia maka transformasi pertama tidak berdampak pada terjemahan label, dan terjemahan label hanya bergantung pada ekstrinsik terbalik kamera. Matriks tampilan digunakan untuk memvisualisasikan label yang diproyeksikan. Untuk mempelajari lebih lanjut tentang transformasi ini dan matriks tampilan, lihatTransformasi Fusi Sensor Ground Truth.

Ground Truth menghitung matriks ekstrinsik ini dengan menggunakan Li DAR dan data pose kamera yang Anda berikan: heading (dalam kuaternion:qx,,, dan) dan (, qyqz,). qw position x y z Untuk kendaraan, biasanya heading dan posisi dijelaskan dalam kerangka acuan kendaraan dalam sistem koordinat dunia dan disebut pose kendaraan ego. Untuk setiap kamera ekstrinsik, Anda dapat menambahkan informasi pose untuk kamera itu. Untuk informasi selengkapnya, lihat Pose.

Matriks Intrinsik

Ground Truth menggunakan matriks ekstrinsik dan intrinsik kamera untuk menghitung metrik tampilan untuk mengubah label ke dan dari adegan 3D ke gambar kamera. Ground Truth menghitung matriks intrinsik kamera menggunakan panjang fokus kamera (fx,fy) dan koordinat pusat optik (cx,cy) yang Anda berikan. Untuk informasi selengkapnya, lihat Intrinsik dan Distorsi.

Distorsi Gambar

Distorsi gambar dapat terjadi karena berbagai alasan. Misalnya, gambar mungkin terdistorsi karena efek barel atau mata ikan. Ground Truth menggunakan parameter intrinsik bersama dengan koefisien distorsi untuk mengubah gambar yang Anda berikan saat membuat pekerjaan pelabelan cloud titik 3D. Jika gambar kamera sudah tidak terdistorsi, semua koefisien distorsi harus disetel ke 0.

Untuk informasi lebih lanjut tentang transformasi yang dilakukan Ground Truth untuk mengubah gambar, lihat. Kalibrasi Kamera: Ekstrinsik, Intrinsik, dan Distorsi

Kendaraan Ego

Untuk mengumpulkan data untuk aplikasi mengemudi otonom, pengukuran yang digunakan untuk menghasilkan data titik cloud dan diambil dari sensor yang dipasang pada kendaraan, atau kendaraan ego. Untuk memproyeksikan penyesuaian label ke dan dari adegan 3D dan gambar 2D, Ground Truth membutuhkan pose kendaraan ego Anda dalam sistem koordinat dunia. Pose kendaraan ego terdiri dari koordinat posisi dan kuaternion orientasi.

Ground Truth menggunakan pose kendaraan ego Anda untuk menghitung matriks rotasi dan transformasi. Rotasi dalam 3 dimensi dapat diwakili oleh urutan 3 rotasi di sekitar urutan sumbu. Secara teori, tiga sumbu apa pun yang mencakup ruang Euclidean 3D sudah cukup. Dalam praktiknya, sumbu rotasi dipilih menjadi vektor dasar. Ketiga rotasi tersebut diharapkan berada dalam kerangka acuan global (ekstrinsik). Ground Truth bukanlah kerangka acuan yang berpusat pada tubuh pendukung (intrinsik) yang melekat pada, dan bergerak dengan, objek di bawah rotasi. Untuk melacak objek, Ground Truth perlu mengukur dari referensi global di mana semua kendaraan bergerak. Saat menggunakan pekerjaan pelabelan awan titik 3D Ground Truth, z menentukan sumbu rotasi (rotasi ekstrinsik) dan sudut Euler yaw berada dalam radian (sudut rotasi).

Pose

Ground Truth menggunakan informasi pose untuk visualisasi 3D dan fusi sensor. Pose informasi yang Anda masukkan melalui file manifes Anda digunakan untuk menghitung matriks ekstrinsik. Jika Anda sudah memiliki matriks ekstrinsik, Anda dapat menggunakannya untuk mengekstrak data sensor dan pose kamera.

Misalnya dalam KITTI dataset mengemudi otonom, modul pykitti python dapat digunakan untuk memuat data. KITTI Dalam dataset dataset.oxts[i].T_w_imu memberikan transformasi DAR ekstrinsik Li untuk frame i th dan dapat dikalikan dengan poin untuk mendapatkannya dalam bingkai dunia -. matmul(lidar_transform_matrix, points) Transformasi ini dapat diubah menjadi posisi (vektor terjemahan) dan heading (dalam kuaternion) Li DAR untuk format file manifes masukan. JSON Transformasi ekstrinsik kamera untuk cam0 i dalam bingkai dapat dihitung dengan inv(matmul(dataset.calib.T_cam0_velo, inv(dataset.oxts[i].T_w_imu))) dan ini dapat diubah menjadi heading dan posisi untuk. cam0

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin= [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R

# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))

# heading in WCS using scipy 
heading = r.as_quat()
print(f"pose:{position}\nheading: {heading}")
Posisi

Dalam file manifes input, position mengacu pada posisi sensor sehubungan dengan bingkai dunia. Jika Anda tidak dapat menempatkan posisi perangkat dalam sistem koordinat dunia, Anda dapat menggunakan DAR data Li dengan koordinat lokal. Demikian pula, untuk kamera video yang dipasang, Anda dapat menentukan posisi dan arah dalam sistem koordinat dunia. Untuk kamera, jika Anda tidak memiliki informasi posisi, silakan gunakan (0, 0, 0).

Berikut ini adalah bidang di objek posisi:

  1. x(float) — x koordinat kendaraan ego, sensor, atau posisi kamera dalam meter.

  2. y(float) — koordinat y kendaraan ego, sensor, atau posisi kamera dalam meter.

  3. z(float) — koordinat z kendaraan ego, sensor, atau posisi kamera dalam meter.

Berikut ini adalah contoh position JSON objek: 

{
    "position": {
        "y": -152.77584902657554,
        "x": 311.21505956090624,
        "z": -10.854137529636024
      }
}
Menuju

Dalam file manifes input, heading adalah objek yang mewakili orientasi perangkat sehubungan dengan bingkai dunia. Nilai heading harus dalam kuaternion. Kuaternion adalah representasi dari orientasi yang konsisten dengan sifat bola geodesik. Jika Anda tidak dapat menempatkan pos sensor di koordinat dunia, silakan gunakan (qx = 0, qy = 0, qz = 0, qw = 1) kuaternion identitas. Demikian pula, untuk kamera, tentukan judul dalam kuarter. Jika Anda tidak dapat memperoleh parameter kalibrasi kamera ekstrinsik, gunakan juga kuaternion identitas.

Bidang dalam heading objek adalah sebagai berikut:

  1. qx(float) - x komponen kendaraan ego, sensor, atau orientasi kamera.

  2. qy(float) - komponen y dari kendaraan ego, sensor, atau orientasi kamera.

  3. qz(float) - komponen z kendaraan ego, sensor, atau orientasi kamera.

  4. qw(float) - w komponen kendaraan ego, sensor, atau orientasi kamera.

Berikut ini adalah contoh heading JSON objek: 

{
    "heading": {
        "qy": -0.7046155108831117,
        "qx": 0.034278837280808494,
        "qz": 0.7070617895701465,
        "qw": -0.04904659893885366
      }
}

Untuk mempelajari selengkapnya, lihat Kuarter dan Posisi Orientasi Hitung.

Kuarter dan Posisi Orientasi Hitung

Ground Truth mensyaratkan bahwa semua orientasi, atau heading, data diberikan dalam kuaternion. Kuaternion adalah representasi dari orientasi yang konsisten dengan sifat bola geodesik yang dapat digunakan untuk perkiraan rotasi. Dibandingkan dengan sudut Euler mereka lebih mudah untuk menulis dan menghindari masalah kunci gimbal. Dibandingkan dengan matriks rotasi mereka lebih kompak, lebih stabil secara numerik, dan lebih efisien.

Anda dapat menghitung kuaternion dari matriks rotasi atau matriks transformasi.

Jika Anda memiliki matriks rotasi (terdiri dari rotasi sumbu) dan vektor translasi (atau asal) dalam sistem koordinat dunia alih-alih matriks transformasi kaku 4x4 tunggal, maka Anda dapat langsung menggunakan matriks rotasi dan vektor terjemahan untuk menghitung kuaternion. Perpustakaan seperti scipy dan pyqaternion dapat membantu. Blok kode berikut menunjukkan contoh menggunakan pustaka ini untuk menghitung kuaternion dari matriks rotasi. 

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin = [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R
# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Alat UI seperti 3D Rotation Converter juga dapat berguna.

Jika Anda memiliki matriks transformasi ekstrinsik 4x4, perhatikan bahwa matriks transformasi berbentuk matriks rotasi dan R T merupakan vektor terjemahan [R T; 0 0 0 1] asal. Itu berarti Anda dapat mengekstrak matriks rotasi dan vektor terjemahan dari matriks transformasi sebagai berikut.

import numpy as np

transformation 
= [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03, 1.71104606e+00],
   [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02, 5.80000039e-01],
   [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01, 9.43144935e-01],
   [              0,               0,               0,              1]]

transformation  = np.array(transformation )
rotation = transformation[0:3][0:3]
translation= transformation[0:3][3]

from scipy.spatial.transform import Rotation as R
# position is the origin translation
position = translation
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Dengan pengaturan Anda sendiri, Anda dapat menghitung matriks transformasi ekstrinsik menggunakanGPS/IMUposisi dan orientasi (lintang, bujur, ketinggian dan gulungan, pitch, yaw) sehubungan dengan sensor Li DAR pada kendaraan ego. Misalnya, Anda dapat menghitung pose dari data KITTI mentah menggunakan pose = convertOxtsToPose(oxts) untuk mengubah data oxts menjadi pose euclidean lokal, yang ditentukan oleh matriks transformasi kaku 4x4. Anda kemudian dapat mengubah matriks transformasi pose ini menjadi kerangka referensi global menggunakan matriks transformasi kerangka referensi dalam sistem koordinat dunia.

struct Quaternion
{
    double w, x, y, z;
};

Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
{
    // Abbreviations for the various angular functions
    double cy = cos(yaw * 0.5);
    double sy = sin(yaw * 0.5);
    double cp = cos(pitch * 0.5);
    double sp = sin(pitch * 0.5);
    double cr = cos(roll * 0.5);
    double sr = sin(roll * 0.5);

    Quaternion q;
    q.w = cr * cp * cy + sr * sp * sy;
    q.x = sr * cp * cy - cr * sp * sy;
    q.y = cr * sp * cy + sr * cp * sy;
    q.z = cr * cp * sy - sr * sp * cy;

    return q;
}

Transformasi Fusi Sensor Ground Truth

Bagian berikut membahas lebih detail tentang transformasi fusi sensor Ground Truth yang dilakukan menggunakan data pose yang Anda berikan.

Li DAR Ekstrinsik

Untuk memproyeksikan ke dan dari DAR adegan Li 3D ke gambar kamera 2D, Ground Truth menghitung metrik proyeksi transformasi kaku menggunakan pose dan heading kendaraan ego. Ground Truth menghitung rotasi dan terjemahan koordinat dunia ke dalam bidang 3D dengan melakukan urutan rotasi dan terjemahan sederhana.

Ground Truth menghitung metrik rotasi menggunakan heading quaternions sebagai berikut:

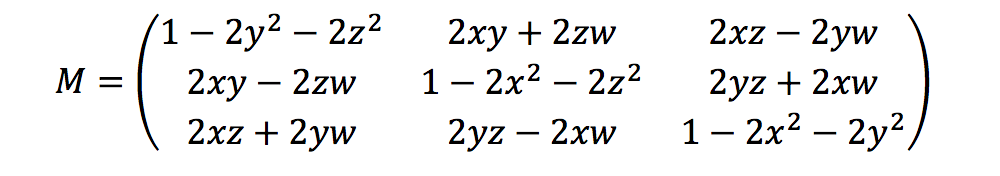
Persamaan: Metrik rotasi awan titik Ground Truth.

Di sini, [x, y, z, w] sesuai dengan parameter dalam heading JSON objek,[qx, qy, qz, qw]. Ground Truth menghitung vektor kolom terjemahan sebagaiT = [poseX, poseY, poseZ]. Maka metrik ekstrinsik hanyalah sebagai berikut:

LiDAR_extrinsic = [R T;0 0 0 1]

Kalibrasi Kamera: Ekstrinsik, Intrinsik, dan Distorsi

Kalibrasi kamera geometris, juga disebut sebagai reseksi kamera, memperkirakan parameter lensa dan sensor gambar dari kamera gambar atau video. Anda dapat menggunakan parameter ini untuk mengoreksi distorsi lensa, mengukur ukuran objek dalam satuan dunia, atau menentukan lokasi kamera di tempat kejadian. Parameter kamera termasuk intrinsik dan koefisien distorsi.

Kamera Ekstrinsik

Jika pose kamera diberikan, maka Ground Truth menghitung ekstrinsik kamera berdasarkan transformasi kaku dari bidang 3D ke bidang kamera. Perhitungannya sama dengan yang digunakan untukLi DAR Ekstrinsik, kecuali bahwa Ground Truth menggunakan pose kamera (positiondanheading) dan menghitung ekstrinsik terbalik.

 camera_inverse_extrinsic = inv([Rc Tc;0 0 0 1]) #where Rc and Tc are camera pose components

Intrinsik dan Distorsi

Beberapa kamera, seperti kamera lubang jarum atau mata ikan, dapat menyebabkan distorsi yang signifikan pada foto. Distorsi ini dapat diperbaiki menggunakan koefisien distorsi dan panjang fokus kamera. Untuk mempelajari lebih lanjut, lihat Kalibrasi kamera Dengan OpenCV di dokumentasi OpenCV.

Ada dua jenis distorsi yang dapat dikoreksi oleh Ground Truth: distorsi radial dan distorsi tangensial.

Distorsi radial terjadi ketika sinar cahaya menekuk lebih dekat tepi lensa daripada di pusat optiknya. Semakin kecil lensa, semakin besar distorsi. Kehadiran distorsi radial bermanifestasi dalam bentuk laras atau efek mata ikan dan Ground Truth menggunakan Formula 1 untuk melepaskannya.

Formula 1:

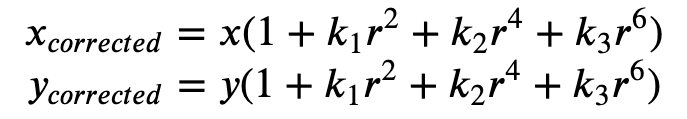
Rumus 1: persamaan untuk x_ {dikoreksi} dan y_ {dikoreksi}, untuk mengubah distorsi radial.

Distorsi tangensial terjadi karena lensa yang digunakan untuk mengambil gambar tidak sejajar sempurna dengan bidang pencitraan. Ini dapat diperbaiki dengan Formula 2.

Rumus 2:

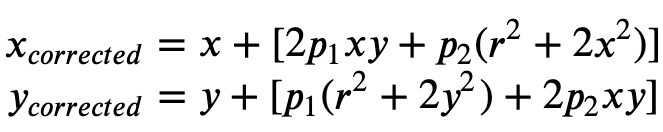
Rumus 2: persamaan untuk x_ {dikoreksi} dan y_ {dikoreksi}, untuk mengoreksi distorsi tangensial.

Dalam file manifes masukan, Anda dapat memberikan koefisien distorsi dan Ground Truth akan menghilangkan distorsi gambar Anda. Semua koefisien distorsi adalah pelampung.

  • k1,, k2k3, k4 — Koefisien distorsi radial. Didukung untuk model kamera mata ikan dan lubang jarum.

  • p1, p2 — Koefisien distorsi tangensial. Didukung untuk model kamera lubang jarum.

Jika gambar sudah tidak terdistorsi, semua koefisien distorsi harus 0 dalam manifes input Anda.

Untuk merekonstruksi gambar yang dikoreksi dengan benar, Ground Truth melakukan konversi unit gambar berdasarkan panjang fokus. Jika panjang fokus umum digunakan dengan rasio aspek tertentu untuk kedua sumbu, seperti 1, dalam rumus atas kita akan memiliki panjang fokus tunggal. Matriks yang berisi empat parameter ini disebut sebagai matriks kalibrasi intrinsik kamera.

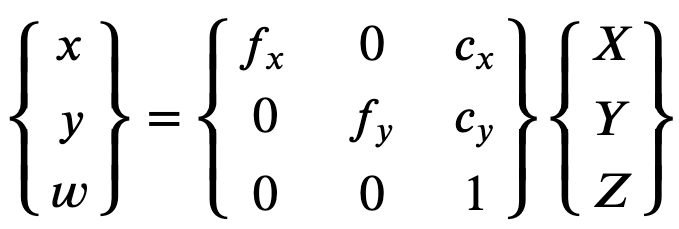
Matriks kalibrasi intrinsik dalam kamera.

Meskipun koefisien distorsi sama terlepas dari resolusi kamera yang digunakan, ini harus diskalakan dengan resolusi saat ini dari resolusi yang dikalibrasi.

Berikut ini adalah nilai float.

  • fx- panjang fokus dalam arah x.

  • fy- panjang fokus ke arah y.

  • cx- x koordinat titik utama.

  • cy- y koordinat titik utama.

Ground Truth menggunakan kamera ekstrinsik dan kamera intrinsik untuk menghitung metrik tampilan seperti yang ditunjukkan pada blok kode berikut untuk mengubah label antara adegan 3D dan gambar 2D.

def generate_view_matrix(intrinsic_matrix, extrinsic_matrix):
    intrinsic_matrix = np.c_[intrinsic_matrix, np.zeros(3)]
    view_matrix = np.matmul(intrinsic_matrix, extrinsic_matrix)
    view_matrix = np.insert(view_matrix, 2, np.array((0, 0, 0, 1)), 0)
    return view_matrix