Le traduzioni sono generate tramite traduzione automatica. In caso di conflitto tra il contenuto di una traduzione e la versione originale in Inglese, quest'ultima prevarrà.
Funzionamento di RCF
Amazon SageMaker AI Random Cut Forest (RCF) è un algoritmo non supervisionato per il rilevamento di punti dati anomali all'interno di un set di dati. Queste sono osservazioni che divergono da dati altrimenti ben strutturati o con motivi. Possono manifestarsi anomalie come picchi non previsti in dati delle serie temporali, interruzioni nelle periodicità o punti dati non classificabili. Sono facili da descrivere in quanto, se visualizzate in un tracciato, sono spesso facilmente distinguibili dai dati "normali". L'inclusione di queste anomalie in un set di dati può aumentare drasticamente la complessità di un'attività di machine learning, poiché i dati "normali" spesso possono essere descritti con un modello semplice.
L'idea principale alla base dell'RCFalgoritmo è creare una foresta di alberi in cui ogni albero venga ottenuto utilizzando una partizione di un campione di dati di addestramento. Ad esempio, viene innanzitutto determinato un esempio casuale dei dati di input. Il campione casuale viene poi partizionato in base al numero di alberi nella foresta. A ogni albero viene assegnata una partizione e organizza tale sottoinsieme di punti in un albero k-d. Il punteggio di anomalia assegnato a un punto dati dall'albero è definito come la modifica prevista della complessità dell'albero in seguito all'aggiunta di tale punto all'albero, che, approssimativamente, è inversamente proporzionale alla profondità del punto risultante nell'albero. Random Cut Forest assegna un punteggio di anomalia calcolando il punteggio medio di ogni albero costituente e adattando il risultato alla dimensione del campione. L'RCFalgoritmo si basa su quello descritto nel riferimento [1].
Campionamento dei dati casuale
Il primo passo dell'RCFalgoritmo consiste nell'ottenere un campione casuale dei dati di allenamento. In particolare, supponiamo di volere un esempio di dimensioni
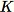 da
da
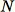 punti di dati totali. Se i dati di addestramento sono abbastanza piccoli, è possibile utilizzare l'intero set di dati e ottenere in modo casuale
punti di dati totali. Se i dati di addestramento sono abbastanza piccoli, è possibile utilizzare l'intero set di dati e ottenere in modo casuale
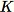 elementi da questo set. Tuttavia, spesso i dati di addestramento sono troppo voluminosi per essere utilizzati tutti in una sola volta e questo approccio non è possibile. Al contrario, utilizziamo una tecnica chiamata "reservoir sampling".
elementi da questo set. Tuttavia, spesso i dati di addestramento sono troppo voluminosi per essere utilizzati tutti in una sola volta e questo approccio non è possibile. Al contrario, utilizziamo una tecnica chiamata "reservoir sampling".
Reservoir sampling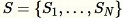 dove gli elementi nel set di dati possono essere osservati solo uno alla volta o in batch. Infatti, reservoir sampling funziona anche quando
dove gli elementi nel set di dati possono essere osservati solo uno alla volta o in batch. Infatti, reservoir sampling funziona anche quando
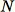 non è noto a priori. Se viene richiesto un solo esempio, ad esempio quando
non è noto a priori. Se viene richiesto un solo esempio, ad esempio quando
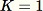 , l'algoritmo è il seguente:
, l'algoritmo è il seguente:
Algoritmo: reservoir sampling
-
Input: set di dati o flusso di dati
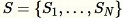
-
Inizializza il campione casuale
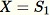
-
Per ogni esempio osservato
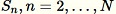 :
:-
Seleziona un numero casuale uniforme
![Equation in text-form: \xi \in [0,1]](images/rcf6.jpg)
-
Se
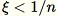
-
Imposta
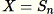
-
-
-
Restituisci
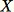
Questo algoritmo seleziona un campione casuale in modo tale che
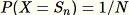 per tutti
per tutti
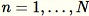 . Quando
. Quando
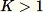 l'algoritmo è più complicato. Inoltre, è necessario fare una distinzione tra campionamento casuale, vale a dire con e senza sostituzione. RCFesegue un campionamento aumentato del serbatoio senza sostituzione sui dati di addestramento sulla base degli algoritmi descritti in [2].
l'algoritmo è più complicato. Inoltre, è necessario fare una distinzione tra campionamento casuale, vale a dire con e senza sostituzione. RCFesegue un campionamento aumentato del serbatoio senza sostituzione sui dati di addestramento sulla base degli algoritmi descritti in [2].
Addestra un RCF modello e produci inferenze
Il passo successivo RCF consiste nel costruire una foresta tagliata a caso utilizzando un campione casuale di dati. In primo luogo, il campione è partizionato in un numero di partizioni di uguale misura che equivalgono al numero di alberi nella foresta. Quindi, ogni partizione viene inviata a un singolo albero. La struttura organizza in modo ricorsivo la propria partizione in un albero binario tramite il partizionamento del dominio dei dati in riquadri di delimitazione.
Questa procedura è illustrato meglio con un esempio. Supponiamo che un determinato albero riceva il seguente set di dati bidimensionale. L'albero corrispondente viene inizializzato in funzione del nodo principale:
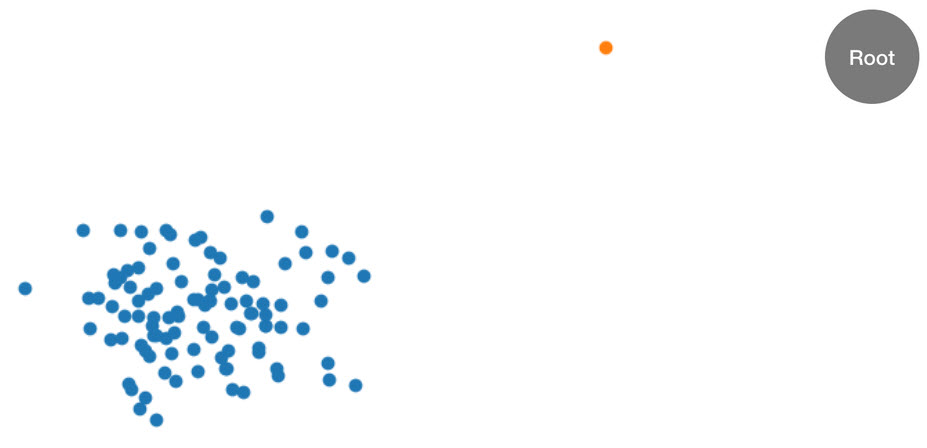
Figura: Un set di dati bidimensionale in cui la maggior parte dei dati si trova in un cluster (blu) ad eccezione di un punto dati anomalo (arancione). L'albero viene inizializzato con un nodo principale.
L'RCFalgoritmo organizza questi dati in un albero calcolando innanzitutto un riquadro di delimitazione dei dati, selezionando una dimensione casuale (dando più peso alle dimensioni con una «varianza» maggiore) e quindi determinando casualmente la posizione di un iperpiano «tagliato» attraverso quella dimensione. I due sottospazi risultanti definiscono il proprio sottoalbero. In questo esempio, il taglio avviene per separare un singolo punto dal resto del campione. Il primo livello di albero binario risultante è composto da due nodi, uno dei quali è formato dal sottoalbero di punti a sinistra del taglio iniziale e l'altro che rappresenta il singolo punto a destra.
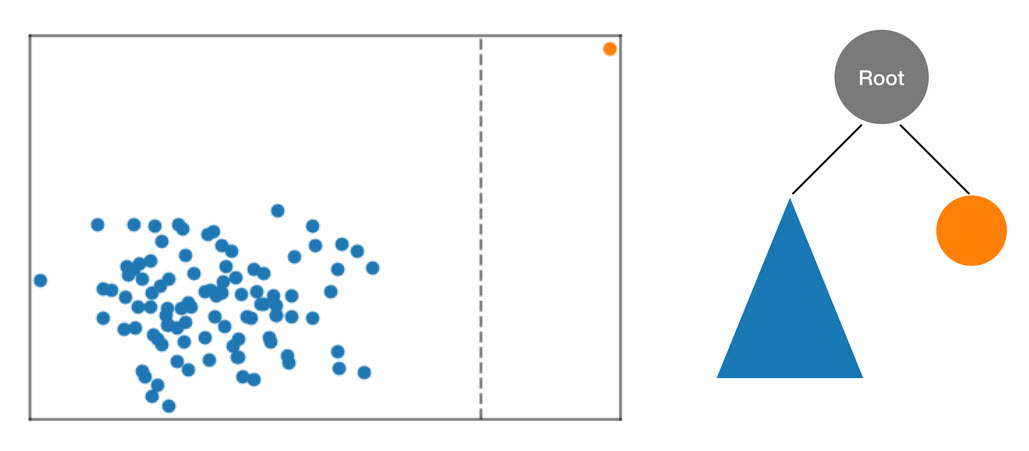
Figura: Un taglio casuale che partiziona il set di dati bidimensionale. Un punto dati anomalo è più soggetto a rimanere isolato in un riquadro di delimitazione a minori profondità rispetto ad altri punti.
I riquadri di delimitazione vengono quindi calcolati per le metà sinistra e destra dei dati e il processo si ripete finché ogni foglia dell'albero non rappresenta un singolo punto dati del campione. Se il singolo punto è sufficientemente lontano, è più probabile che un taglio casuale ne comporti l'isolamento. Da questa osservazione è possibile concludere che la profondità dell'albero è, in generale, inversamente proporzionale al punteggio di anomalia.
Quando si esegue l'inferenza utilizzando un RCF modello addestrato, il punteggio di anomalia finale viene riportato come media tra i punteggi riportati da ciascun albero. Spesso accade che il nuovo punto dati non risiede già nell'albero. Per determinare il punteggio associato al nuovo punto, il punto dati viene inserito nell'albero specificato e l'albero viene riassemblato in modo efficiente (e temporaneo) come al momento del processo di addestramento descritto sopra. In altre parole, nell'albero prodotto è come se il punto dati di input sia stato un membro del campione utilizzato per la costruzione iniziale dell'albero. Il punteggio segnalato è inversamente proporzionale alla profondità del punto di input all'interno dell'albero.
Scelta degli iperparametri
Gli iperparametri principali utilizzati per ottimizzare il RCF modello sono e. num_trees num_samples_per_tree L'aumento di num_trees ha l'effetto di ridurre il rumore osservato nei punteggi di anomalie poiché il punteggio finale corrisponde alla media dei punteggi riportati da ciascun albero. Mentre il valore ottimale dipende dall'applicazione, ti consigliamo di utilizzare 100 alberi per iniziare con un equilibrio tra il rumore dei valori e la complessità del modello. Il tempo di inferenza è proporzionale al numero degli alberi. Sebbene anche la durata dell’addestramento ne sia interessata, è dominata dall'algoritmo reservoir sampling descritto sopra.
Il parametro num_samples_per_tree è correlato alla densità stimata di anomalie nel set di dati. In particolare, num_samples_per_tree deve essere scelto in modo tale che 1/num_samples_per_tree si avvicini al rapporto tra i dati anomali e i dati normali. Ad esempio, se in ciascun albero vengono utilizzati 256 campioni, ci aspetteremo che i nostri dati contengano 1/256 anomalie o occupino approssimativamente lo 0,4% del tempo. Un valore ottimale per questo iperparametro dipende dall'applicazione.
Riferimenti
-
Sudipto Guha, Nina Mishra, Gourav Roy e Okke Schrijvers. "Robust random cut forest based anomaly detection on streams." In International Conference on Machine Learning, pp. 2712-2721. 2016.
-
Byung-Hoon Park, George Ostrouchov, Nagiza F. Samatova e Al Geist. "Reservoir-based random sampling with replacement from data stream." In Atti della Conferenza SIAM internazionale sul data mining del 2004, pagg. 492-496. Society for Industrial and Applied Mathematics, 2004.