翻訳は機械翻訳により提供されています。提供された翻訳内容と英語版の間で齟齬、不一致または矛盾がある場合、英語版が優先します。
PCA の仕組み
プリンシパルコンポーネント分析 (PCA) は、可能な限り多くの情報を保持しながら、データセット内の次元 (特徴量の数) を減らす学習アルゴリズムです。
PCA は、元の特徴の複合であるコンポーネント と呼ばれる新しい特徴セットを見つけることで、次元性を軽減します。これは互いに相関しません。最初の成分はデータ内で考えられる最大の変動性、2 番目の成分は 2 番目に大きな変動性と続きます。
これは教師なしの次元縮退アルゴリズムです。教師なしの学習では、トレーニングデータセット内のオブジェクトに関連付けられている可能性のあるラベルは使用されません。
行
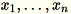の各次元が 1 * d である行列を入力すると、データはミニバッチの行に分割され、トレーニングノード (ワーカー) に分配されます。各ワーカーは、その後そのデータのサマリーを計算します。計算終了後、個々のワーカーのサマリーは 1 つの解に統一されます。
モード
Amazon SageMaker PCA アルゴリズムは、状況に応じて、2 つのモードのいずれかを使用してこれらの概要を計算します。
-
regular: 疎データと標準的な数の観測および特徴を備えたデータセットの場合。
-
randomized: 多数の観測および特徴の両方を備えたデータセットの場合。このモードは近似アルゴリズムを使用します。
アルゴリズムの最後のステップでは、統一解に対して特異値分解を実行し、主成分はそこから派生します。
モード 1: Regular
ワーカーは、
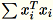と
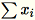の両方を計算します。
注記
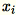は行ベクトル 1 * d であるため、
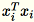は行列です (スカラーではありません)。コード内で行ベクトルを使用すると、キャッシュを効率的に取得できます。
共分散行列は
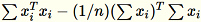という式で計算され、その上位の特異ベクトル num_components がモデルを形成します。
注記
subtract_mean が False である場合、
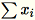の計算と減算は回避します。
ベクトルの次元 d が十分に小さく、
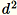がメモリに収まる場合に、このアルゴリズムを使用します。
モード 2: Randomized
入力データセット内の特徴の数が多い場合は、共分散行列を近似するメソッドを使用します。次元 b * d のすべてのミニバッチ
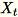において、各ミニバッチで乗算する行列 (num_components + extra_components) * b をランダムに初期化し、行列 (num_components + extra_components) * d を作成します。これらの行列の合計はワーカーによって計算され、サーバーは最終(num_components + extra_components) * d行列SVDで実行されます。右上のその num_components 特異ベクトルは、入力行列の上位の特異ベクトルの近似値です。
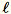
= num_components + extra_components であるとします。次元 b * d のミニバッチ
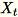が指定されると、ワーカーは次元
のランダム行列
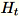を抽出します。環境が GPUまたは を使用するかどうか、CPUおよびディメンションサイズに応じて、行列は各エントリが +-1または であるランダムな符号行列です FJLT (高速Johnson Lindenstrauss 変換。詳細については、FJLT「変換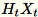
を計算し、
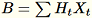を保持します。ワーカーは、
、
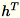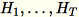の列の合計 (T はミニバッチの総数)、s (すべての入力行の合計) も保持します。データの全シャードを処理した後、ワーカーはサーバーに B、h、s、および n (入力行の合計数) を送信します。
サーバーへの各種入力は
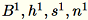と表記します。サーバーは、B、h、s、n (それぞれの入力の合計) を計算します。さらに
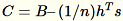を計算し、その特異値分解を見つけます。右上の特異ベクトルと C の特異値が問題に対する近似解として使用されます。
