As traduções são geradas por tradução automática. Em caso de conflito entre o conteúdo da tradução e da versão original em inglês, a versão em inglês prevalecerá.

Como RCF funciona

O Amazon SageMaker Random Cut Forest (RCF) é um algoritmo não supervisionado para detectar pontos de dados anômalos em um conjunto de dados. Trata-se de observações que divergem de outros dados padronizados ou bem-estruturados. As anomalias podem se manifestar como picos inesperados em dados de séries temporais, pausas na periodicidade ou pontos de dados inclassificáveis. São de fácil descrição quando visualizados em um gráfico, pois frequentemente se distinguem dos dados "normais". A inclusão dessas anomalias em um conjunto de dados pode aumentar drasticamente a complexidade de uma tarefa de machine learning, já que os dados "normais" podem ser descritos com um modelo simples.

A ideia principal por trás do RCF algoritmo é criar uma floresta de árvores onde cada árvore é obtida usando uma partição de uma amostra dos dados de treinamento. Por exemplo, uma amostra aleatória dos dados de entrada é determinada pela primeira vez. A amostra aleatória é, então, particionada de acordo com o número de árvores na floresta. Cada árvore recebe uma partição e organiza esse subconjunto de pontos em uma árvore k-d. A pontuação de anomalia atribuída a um ponto de dados pela árvore é definida como a alteração esperada na complexidade dessa árvore, resultando na inclusão do ponto à árvore. Além disso, tal resultado, na aproximação, é inversamente proporcional à profundidade resultante do ponto na árvore. Para atribuir uma pontuação de anomalia, o Random Cut Forest calcula a pontuação média de cada árvore integrante e escala o resultado em relação ao tamanho da amostra. O RCF algoritmo é baseado no descrito na referência [1].

Obter amostra de dados de forma aleatória

A primeira etapa do RCF algoritmo é obter uma amostra aleatória dos dados de treinamento. Em particular, suponha que queiramos uma amostra de tamanho do total de 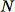pontos de dados. Se os dados de treinamento forem pequenos o suficiente, todo o conjunto de dados poderá ser usado, poderíamos desenhar aleatoriamente elementos desse conjunto. No entanto, os dados de treinamento frequentemente são muito grandes para se encaixarem todos de uma vez, e essa abordagem não é viável. Em vez disso, usamos uma técnica chamada de amostragem de reservatório.

A amostragem de reservatório é um algoritmo para o desenho eficiente de amostras aleatórias de um conjunto de dados , em que os elementos no conjunto de dados só podem ser observados um de cada vez ou em lotes. De fato, a amostragem de reservatório funciona mesmo quando 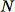não é conhecido a priori. Se apenas uma amostra for solicitada, como quando 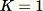, o algoritmo será:

Algoritmo: Amostragem de reservatório

Esse algoritmo seleciona uma amostra aleatória, de modo que para todos os . Quando , o algoritmo é mais complicado. Além disso, é necessário estabelecer uma distinção entre a amostragem aleatória que está com substituição e a que está sem. RCFrealiza uma amostragem aumentada do reservatório sem substituição dos dados de treinamento com base nos algoritmos descritos em [2].

Treine um RCF modelo e produza inferências

A próxima etapa RCF é construir uma floresta cortada aleatoriamente usando a amostra aleatória de dados. Primeiramente, a amostra é particionada em uma série de partições de tamanho igual, na mesma quantidade de árvores da floresta. Em seguida, cada partição é enviada para uma árvore individual. Para organizar recursivamente a partição em uma árvore binária, a árvore particiona o domínio de dados em caixas delimitadoras.

Esse procedimento é mais bem ilustrado com um exemplo. Digamos que uma árvore receba o seguinte conjunto de dados bidimensional. A árvore correspondente é inicializada para o nó raiz:

Figura: Um conjunto de dados bidimensional em que a maioria dos dados está em um cluster (azul), exceto por um ponto de dados anômalo (laranja). A árvore é inicializada com um nó raiz.

O RCF algoritmo organiza esses dados em uma árvore calculando primeiro uma caixa delimitadora dos dados, selecionando uma dimensão aleatória (dando mais peso às dimensões com maior “variância”) e, em seguida, determinando aleatoriamente a posição de um hiperplano “cortado” nessa dimensão. Os dois subespaços resultantes definem a própria subárvore deles. Nesse exemplo, o corte ocorre para separar um ponto isolado do restante da amostra. O primeiro nível da árvore binária resultante consiste em dois nós: um com a subárvore de pontos à esquerda do corte inicial, e o outro representando o único ponto à direita.

Figura: Um corte aleatório particionando o conjunto de dados bidimensional. É mais provável que um ponto de dados anormal resida isoladamente em uma caixa delimitadora, em uma profundidade menor do que outros pontos na árvore.

As caixas delimitadoras são então calculadas para as metades esquerda e direita dos dados, e o processo é repetido até que todas as folhas da árvore represente um único ponto de dados da amostra. Observe que, se o ponto único estiver suficientemente longe, é mais provável que um corte aleatório resulte em seu isolamento. Essa observação fornece a intuição de que a profundidade da árvore é, a grosso modo, inversamente proporcional à pontuação de anomalia.

Ao realizar a inferência usando um RCF modelo treinado, a pontuação final da anomalia é relatada como a média das pontuações relatadas por cada árvore. Observe que é frequente o fato de que o novo ponto de dados ainda não reside na árvore. Para determinar a pontuação associada ao novo ponto, o ponto de dados é inserido na árvore em questão, que, por sua vez, é eficientemente (e temporariamente) remontada de uma maneira equivalente ao processo de treinamento descrito acima. Ou seja, a árvore resultante é como se o ponto de dados de entrada fosse um membro da amostra usada para construir a árvore no começo. A pontuação registrada é inversamente proporcional à profundidade do ponto de entrada na árvore.

Escolher hiperparâmetros

Os hiperparâmetros primários usados para ajustar o RCF modelo são num_trees e. num_samples_per_tree Se você aumentar o num_trees, o ruído observado em pontuações de anomalia será reduzido, já que a última pontuação é a média das pontuações registradas por cada árvore. Embora o valor ideal dependa do aplicativo, recomendamos começar usando 100 árvores, para que haja equilíbrio entre o ruído das pontuações e a complexidade do modelo. Observe que o tempo de inferência é proporcional ao número de árvores. Embora o tempo de treinamento também seja afetado, ele é controlado pelo algoritmo de amostragem de reservatório descrito acima.

O parâmetro num_samples_per_tree está relacionado à densidade esperada de anomalias no conjunto de dados. Especificamente, num_samples_per_tree deve ser escolhido de modo que 1/num_samples_per_tree se aproxime da proporção entre dados anormais e dados normais. Por exemplo, se 256 amostras forem usadas em cada árvore, o esperado é que os dados contenham anomalias de 1/256 ou aproximadamente 0,4% do tempo. Novamente, um valor ideal para esse hiperparâmetro depende do aplicativo.

Referências