Noções básicas sobre sistemas de coordenadas e fusão de sensores

Os dados da nuvem de pontos estão sempre localizados em um sistema de coordenadas. Esse sistema de coordenadas pode ser local para o veículo ou o dispositivo que está detectando o ambiente, ou pode ser um sistema de coordenadas mundial. Ao usar trabalhos de rotulagem de nuvem de pontos 3D do Ground Truth, todas as anotações são geradas usando o sistema de coordenadas dos dados de entrada. Para alguns tipos de tarefa de trabalho de rotulagem e atributos, é necessário fornecer dados em um sistema de coordenadas mundial.

Neste tópico, você aprenderá o seguinte:

Requisitos do sistema de coordenadas para trabalhos de rotulagem

Se os dados da nuvem de pontos foram coletados em um sistema de coordenadas local, é possível usar uma matriz extrínseca do sensor usado para coletar os dados a fim de convertê-los em um sistema de coordenadas mundial ou em um quadro de referência global. Se não conseguir obter um extrínseco para os dados da nuvem de pontos e, como resultado, não conseguir obter nuvens de pontos em um sistema de coordenadas mundial, você poderá fornecer dados da nuvem de pontos em um sistema de coordenadas local para detecção de objetos da nuvem de pontos 3D e tipos de tarefas de segmentação semântica.

Para o rastreamento de objetos, é necessário fornecer dados da nuvem de pontos em um sistema de coordenadas mundial. Isso ocorre porque quando você está rastreando objetos em vários quadros, o próprio veículo ego está se movendo no mundo e, portanto, todos os quadros precisam de um ponto de referência.

Se você incluir dados da câmera para fusão de sensores, é recomendável fornecer poses da câmera no mesmo sistema de coordenadas mundial que o sensor 3D (como um sensor LiDAR).

Usar dados da nuvem de pontos em um sistema de coordenadas mundial

Esta seção explica o que é um sistema de coordenadas mundial (WCS), também chamado de quadro de referência global, e explica como é possível fornecer dados da nuvem de pontos em um sistema de coordenadas mundial.

O que é um sistema de coordenadas mundial?

Um WCS ou quadro de referência global é um sistema de coordenadas universal fixo no qual os sistemas de coordenadas de veículos e de sensores são colocados. Por exemplo, se vários quadros da nuvem de pontos estiverem localizados em sistemas de coordenadas diferentes porque foram coletados de dois sensores, um WCS poderá ser usado para converter todas as coordenadas nesses quadros da nuvem de pontos em um único sistema de coordenadas, em que todos os quadros têm a mesma origem (0,0,0). Essa transformação é feita convertendo a origem de cada quadro para a origem do WCS usando um vetor de conversão e girando os três eixos (normalmente x, y e z) para a orientação correta usando uma matriz de rotação. Essa transformação do corpo rígido é chamada de transformação homogênea.

Um sistema de coordenadas mundiais é importante no planejamento global de caminhos, localização, mapeamento e simulações de cenários de condução. O Ground Truth usa o sistema cartesiano de coordenadas mundiais destro, como o definido na ISO 8855, em que o eixo x avança em direção ao movimento do carro, o eixo y fica à esquerda e o eixo z aponta para cima do solo.

O quadro de referência global depende dos dados. Alguns conjuntos de dados usam a posição LiDAR no primeiro quadro como origem. Nesse cenário, todos os quadros usam o primeiro quadro como referência e o cabeçalho e a posição do dispositivo estarão próximos da origem no primeiro quadro. Por exemplo, os conjuntos de dados KITTI têm o primeiro quadro como referência para coordenadas mundiais. Outros conjunto de dados usam uma posição de dispositivo que é diferente da origem.

Observe que este não é o sistema de coordenadas GPS/IMU, que normalmente é girado em 90 graus ao longo do eixo z. Se os dados da nuvem de pontos estiverem em um sistema de coordenadas GPS/IMU (como OxTS no conjunto de dados AV KITTI de código aberto), será necessário transformar a origem em um sistema de coordenadas mundial (geralmente o sistema de coordenadas de referência do veículo). Essa transformação é aplicada multiplicando os dados por métricas de transformação (a matriz de rotação e o vetor de conversão). Isso transformará os dados de seu sistema de coordenadas original em um sistema de coordenadas de referência global. Saiba mais sobre essa transformação na próxima seção.

Converter dados da nuvem de pontos 3D em um WCS

O Ground Truth pressupõe que os dados da nuvem de pontos já tenham sido transformados em um sistema de coordenadas de referência de sua escolha. Por exemplo, é possível escolher o sistema de coordenadas de referência do sensor (como o LiDAR) como seu sistema de coordenadas de referência global. Também é possível tirar nuvens de pontos de vários sensores e transformá-las da visualização do sensor para a visualização do sistema de coordenadas de referência do veículo. Use a matriz extrínseca de um sensor, composta por uma matriz de rotação e um vetor de conversão, para converter os dados da nuvem de pontos em um WCS ou em um quadro de referência global.

Coletivamente, o vetor de conversão e a matriz de rotação podem ser usados para formar uma matriz extrínseca, que pode ser usada para converter dados de um sistema de coordenadas local para um WCS. Por exemplo, a matriz extrínseca LiDAR pode ser composta da seguinte forma, em que R é a matriz de rotação e T é o vetor de conversão:

LiDAR_extrinsic = [R T;0 0 0 1]

Por exemplo, o conjunto de dados KITTI de condução autônoma inclui uma matriz de rotação e um vetor de conversão para a matriz de transformação extrínseca LiDAR de cada quadro. O módulo pykitti do Python pode ser usado para carregar os dados KITTI e, no conjunto de dados, dataset.oxts[i].T_w_imu fornece a transformação extrínseca LiDAR para o i^º quadro, que pode ser multiplicado por pontos nesse quadro a fim de convertê-los em um quadro mundial: np.matmul(lidar_transform_matrix, points). Multiplicar um ponto no quadro LiDAR com uma matriz extrínseca LiDAR transforma-o em coordenadas mundiais. Multiplicar um ponto no quadro mundial com a matriz extrínseca da câmera fornece as coordenadas de pontos no quadro de referência da câmera.

O exemplo de código a seguir demonstra como você pode converter quadros da nuvem de pontos do conjunto de dados KITTI em um WCS.

import pykitti
import numpy as np

basedir = '/Users/nameofuser/kitti-data'
date = '2011_09_26'
drive = '0079'

# The 'frames' argument is optional - default: None, which loads the whole dataset.
# Calibration, timestamps, and IMU data are read automatically. 
# Camera and velodyne data are available via properties that create generators
# when accessed, or through getter methods that provide random access.
data = pykitti.raw(basedir, date, drive, frames=range(0, 50, 5))

# i is frame number
i = 0

# lidar extrinsic for the ith frame
lidar_extrinsic_matrix = data.oxts[i].T_w_imu

# velodyne raw point cloud in lidar scanners own coordinate system
points = data.get_velo(i)

# transform points from lidar to global frame using lidar_extrinsic_matrix
def generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix):
    tps = []
    for point in points:
        transformed_points = np.matmul(lidar_extrinsic_matrix, np.array([point[0], point[1], point[2], 1], dtype=np.float32).reshape(4,1)).tolist()
        if len(point) > 3 and point[3] is not None:
            tps.append([transformed_points[0][0], transformed_points[1][0], transformed_points[2][0], point[3]])
       
    return tps
    
# customer transforms points from lidar to global frame using lidar_extrinsic_matrix
transformed_pcl = generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix)    

Fusão de sensores

O Ground Truth oferece apoio à fusão de sensores de dados da nuvem de pontos com até oito entradas de câmera de vídeo. Esse atributo permite que os rotuladores humanos visualizem o quadro da nuvem de pontos 3D lado a lado com o quadro de vídeo sincronizado. Além de fornecer mais contexto visual para rotulagem, a fusão de sensores permite aos operadores ajustar anotações na cena 3D e em imagens 2D e o ajuste é projetado na outra visualização. O vídeo a seguir demonstra um trabalho de rotulagem de nuvem de pontos 3D com LiDAR e fusão de sensores de câmera.

Para obter melhores resultados, ao usar a fusão de sensores, a nuvem de pontos deve estar em um WCS. O Ground Truth usa o sensor (como o LiDAR), câmera e informações de pose do veículo ego para calcular matrizes extrínsecas e intrínsecas para fusão de sensores.

Matriz extrínseca

O Ground Truth usa matrizes extrínsecas e intrínsecas de sensores (como o LiDAR) para projetar objetos de e para o quadro de referência dos dados da nuvem de pontos para o quadro de referência da câmera.

Por exemplo, para projetar um rótulo da nuvem de pontos 3D para o plano de imagem da câmera, o Ground Truth transforma pontos 3D do próprio sistema de coordenadas do LiDAR para o sistema de coordenadas da câmera. Isso normalmente é feito transformando primeiro os pontos 3D do próprio sistema de coordenadas do LiDAR em um sistema de coordenadas mundial (ou um quadro de referência global) usando a matriz extrínseca do LiDAR. O Ground Truth então usa o extrínseco inverso da câmera (que converte pontos de um quadro de referência global para o quadro de referência da câmera) para transformar os pontos 3D do sistema de coordenadas mundiais obtidos na etapa anterior no plano da imagem da câmera. A matriz extrínseca do LiDAR também pode ser usada para transformar dados 3D em um sistema de coordenadas mundial. Se os dados 3D já estiverem transformados em sistema de coordenadas mundiais, então a primeira transformação não terá nenhum impacto na conversão de rótulos, e ela dependerá apenas da extrínseca inversa da câmera. Uma matriz de visualização é usada para visualizar rótulos projetados. Para saber mais sobre essas transformações e sobre a matriz de visualização, consulte Transformações de fusão do sensor Ground Truth.

O Ground Truth calcula essas matrizes extrínsecas usando o LiDAR e os dados de pose de câmera que você fornece: heading (em quaterniões: qx, qy, qz e qw) e position (x, y, z). Para o veículo, normalmente o rumo e a posição são descritos no quadro de referência do veículo em um sistema de coordenadas mundial e são chamados de pose do veículo ego. Para cada câmera extrínseca, é possível adicionar informações de pose para essa câmera. Para obter mais informações, consulte Pose.

Matriz intrínseca

O Ground Truth usa as matrizes extrínsecas e intrínsecas da câmera para calcular métricas de visualização e transformar rótulos de e para a cena 3D em imagens de câmera. O Ground Truth calcula a matriz intrínseca da câmera usando a distância focal da câmera (fx, fy) e as coordenadas do centro óptico (cx, cy) que você fornece. Para obter mais informações, consulte Intrínseca e distorção.

Distorção de imagem

A distorção de imagem pode ocorrer por uma variedade de razões. Por exemplo, as imagens podem ficar distorcidas devido aos efeitos barril ou olho de peixe. O Ground Truth usa parâmetros intrínsecos junto com o coeficiente de distorção para não distorcer as imagens que você fornece ao criar trabalhos de rotulagem de nuvem de pontos 3D. Se a distorção de uma imagem da câmera já tiver sido corrigida, todos os coeficientes de distorção deverão estar definidos como 0.

Para obter mais informações sobre as transformações que o Ground Truth executa para corrigir a distorção de imagens, consulte Calibrações da câmera: extrínseca, intrínseca e distorção.

Veículo ego

A fim de coletar dados para aplicações de condução autônoma, as medições usadas para gerar dados da nuvem de pontos são coletadas de sensores montados em um veículo, ou o veículo ego. Para projetar ajustes de rótulo de e para a cena 3D e imagens 2D, o Ground Truth precisa da pose do veículo ego em um sistema de coordenadas mundial. A pose do veículo ego é composta por coordenadas de posição e pelo quaternião de orientação.

O Ground Truth usa a pose do veículo ego para calcular matrizes de rotação e de transformações. As rotações em três dimensões podem ser representadas por uma sequência de três rotações em torno de uma sequência de eixos. Em teoria, quaisquer três eixos que abrangem o espaço euclidiano 3D são suficientes. Na prática, os eixos de rotação são escolhidos para serem os vetores de base. Espera-se que as três rotações estejam em um quadro de referência global (extrínseco). O Ground Truth não é compatível com um quadro de referência centrado no corpo (intrínseco) que está ligado e se move com o objeto em rotação. Para rastrear objetos, o Ground Truth precisa medir a partir de uma referência global na qual todos os veículos estão se movendo. Ao usar trabalhos de rotulagem de nuvem de pontos 3D do Ground Truth, z especifica o eixo de rotação (rotação extrínseca) e os ângulos de guinada de Euler estão em radianos (ângulo de rotação).

Pose

O Ground Truth usa informações de pose para visualizações 3D e fusão de sensores. As informações de pose inseridas pelo arquivo de manifesto são usadas para calcular matrizes extrínsecas. Se você já tem uma matriz extrínseca, é possível usá-la para extrair dados de pose da câmera e do sensor.

Por exemplo, no conjunto de dados KITTI de condução autônoma, o módulo pykitti do Python pode ser usado para carregar os dados KITTI. No conjunto de dados, dataset.oxts[i].T_w_imu fornece a transformação extrínseca do LiDAR para o i^º quadro e ele pode ser multiplicado pelos pontos para obtê-los em um quadro mundial: matmul(lidar_transform_matrix, points). Essa transformação pode ser convertida em posição (vetor de conversão) e cabeçalho (em quaternião) do LiDAR para o formato JSON do arquivo de manifesto de entrada. A transformação extrínseca da câmera para o cam0 no i^º quadro pode ser calculada por inv(matmul(dataset.calib.T_cam0_velo, inv(dataset.oxts[i].T_w_imu))) e isso pode ser convertido em cabeçalho e posição para cam0.

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin= [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R

# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))

# heading in WCS using scipy 
heading = r.as_quat()
print(f"pose:{position}\nheading: {heading}")

Posição

No arquivo manifesto de entrada, position se refere à posição do sensor em relação a um quadro mundial. Se não conseguir colocar a posição do dispositivo em um sistema de coordenadas mundial, você poderá usar dados do LiDAR com coordenadas locais. Da mesma forma, para câmeras de vídeo montadas, é possível especificar a posição e o cabeçalho em um sistema de coordenadas mundial. Para a câmera, se você não tiver informações de posição, use (0, 0, 0).

Estes são os campos no objeto de posição:

Veja a seguir um exemplo de um objeto JSON position.

{
    "position": {
        "y": -152.77584902657554,
        "x": 311.21505956090624,
        "z": -10.854137529636024
      }
}

Cabeçalho

No arquivo manifesto de entrada, heading é um objeto que representa a orientação de um dispositivo em relação ao quadro mundial. Os valores do cabeçalho devem estar em quaternião. Um quaternião é uma representação da orientação consistente com as propriedades esféricas geodésicas. Se você não conseguir colocar o cabeçalho do sensor nas coordenadas mundiais, use o quaternião de identidade (qx = 0, qy = 0, qz = 0, qw = 1). Da mesma forma, para câmeras, especifique o cabeçalho em quaterniões. Se você não conseguir obter parâmetros extrínsecos de calibração da câmera, use também o quaternião de identidade.

Os campos no objeto heading são os seguintes:

Veja a seguir um exemplo de um objeto JSON heading.

{
    "heading": {
        "qy": -0.7046155108831117,
        "qx": 0.034278837280808494,
        "qz": 0.7070617895701465,
        "qw": -0.04904659893885366
      }
}

Para saber mais, consulte Calcular a posição e os quaterniões de orientação.

Calcular a posição e os quaterniões de orientação

O Ground Truth requer que todos os dados de orientação, ou de cabeçalho, sejam fornecidos em quaterniões. Um quaternião é uma representação da orientação consistente com as propriedades esféricas geodésicas que podem ser usadas para se aproximar da rotação. Em comparação com os ângulos de Euler eles são mais simples de compor e evitar o problema de gimbal lock. Em comparação com matrizes de rotação, eles são mais compactos, numericamente mais estáveis e mais eficientes.

É possível calcular quaterniões a partir de uma matriz de rotação ou de uma matriz de transformação.

Se tiver uma matriz de rotação (composta pelas rotações do eixo) e um vetor de conversão (ou origem) no sistema de coordenadas mundial em vez de uma única matriz de transformação rígida 4x4, você poderá usar diretamente a matriz de rotação e o vetor de conversão para calcular quaterniões. Bibliotecas como scipy e pyqaternion podem ajudar. O bloco de código a seguir mostra um exemplo que usa essas bibliotecas para calcular quaterniões a partir de uma matriz de rotação.

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin = [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R
# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Uma ferramenta de interface do usuário como 3D Rotation Converter também pode ser útil.

Se você tiver uma matriz de transformação extrínseca 4x4, observe que a matriz de transformação está na forma [R T; 0 0 0 1], em que R é a matriz de rotação e T é o vetor de conversão de origem. Isso significa que você pode extrair a matriz de rotação e o vetor de conversão da matriz de transformação da maneira indicada a seguir.

import numpy as np

transformation 
= [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03, 1.71104606e+00],
   [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02, 5.80000039e-01],
   [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01, 9.43144935e-01],
   [              0,               0,               0,              1]]

transformation  = np.array(transformation )
rotation = transformation[0:3,0:3]
translation= transformation[0:3,3]

from scipy.spatial.transform import Rotation as R
# position is the origin translation
position = translation
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Com sua própria configuração, é possível calcular uma matriz de transformação extrínseca usando a posição e a orientação GPS/IMU (latitude, longitude, altitude e rolagem, inclinação, guinada) em relação ao sensor do LiDAR no veículo ego. Por exemplo, é possível calcular a pose dos dados brutos KITTI usando pose = convertOxtsToPose(oxts) para transformar os dados oxts em poses euclidianas locais, especificadas por matrizes de transformação rígidas 4x4. Depois, é possível transformar essa matriz de transformação de pose em um quadro de referência global usando a matriz de transformação de quadros de referência no sistema de coordenadas mundial.

struct Quaternion
{
    double w, x, y, z;
};

Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
{
    // Abbreviations for the various angular functions
    double cy = cos(yaw * 0.5);
    double sy = sin(yaw * 0.5);
    double cp = cos(pitch * 0.5);
    double sp = sin(pitch * 0.5);
    double cr = cos(roll * 0.5);
    double sr = sin(roll * 0.5);

    Quaternion q;
    q.w = cr * cp * cy + sr * sp * sy;
    q.x = sr * cp * cy - cr * sp * sy;
    q.y = cr * sp * cy + sr * cp * sy;
    q.z = cr * cp * sy - sr * sp * cy;

    return q;
}

Transformações de fusão do sensor Ground Truth

As seções a seguir entram em mais detalhes sobre as transformações de fusão de sensores do Ground Truth que são executadas usando os dados de pose fornecidos.

Extrínseca do LiDAR

Para projetar de e para uma cena do LiDAR 3D para uma imagem de câmera 2D, o Ground Truth calcula as métricas rígidas de projeção de transformação usando a pose e o rumo do veículo-ego. O Ground Truth calcula a rotação e translação de coordenadas mundiais no plano 3D fazendo uma sequência simples de rotações e translação.

O Ground Truth calcula métricas de rotação usando os quaterniões de cabeçalho da seguinte forma:

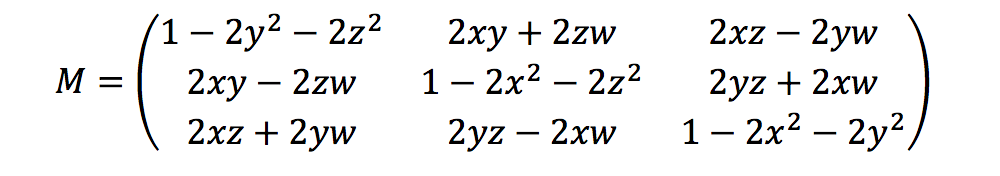
Aqui, [x, y, z, w] corresponde aos parâmetros no headingobjeto JSON, [qx, qy, qz, qw]. O Ground Truth calcula o vetor da coluna de tradução como T = [poseX, poseY, poseZ]. Depois, as métricas extrínsecas são simplesmente as seguintes:

LiDAR_extrinsic = [R T;0 0 0 1]

Calibrações da câmera: extrínseca, intrínseca e distorção

A calibração geométrica da câmera, também chamada de ressecção da câmera, estima os parâmetros de uma lente e de um sensor de imagem de uma câmera de imagem ou vídeo. É possível usar esses parâmetros para corrigir a distorção da lente, medir o tamanho de um objeto em unidades mundiais ou determinar a localização da câmera na cena. Os parâmetros da câmera incluem coeficientes intrínsecos e de distorção.

Câmera extrínseca

Se a pose da câmera for fornecida, o Ground Truth calculará a câmera extrínseca com base em uma transformação rígida do plano 3D no plano da câmera. O cálculo é o mesmo que o usado para o Extrínseca do LiDAR, exceto que o Ground Truth usa a pose de câmera (position e heading) e calcula a extrínseca inversa.

 camera_inverse_extrinsic = inv([Rc Tc;0 0 0 1]) #where Rc and Tc are camera pose components

Intrínseca e distorção

Algumas câmeras, como câmeras pinhole ou olho de peixe, podem apresentar distorção significativa nas fotos. Essa distorção pode ser corrigida usando coeficientes de distorção e a distância focal da câmera. Para saber mais, consulte Calibração da câmera com o OpenCV na documentação do OpenCV.

Há dois tipos de distorção que o Ground Truth pode corrigir: distorção radial e distorção tangencial.

A distorção radial ocorre quando os raios de luz se dobram mais perto das bordas de uma lente do que em seu centro óptico. Quanto menor a lente, maior a distorção. A presença da distorção radial se manifesta na forma do efeito barril ou olho de peixe e o Ground Truth usa a Fórmula 1 para corrigir a distorção.

Fórmula 1:

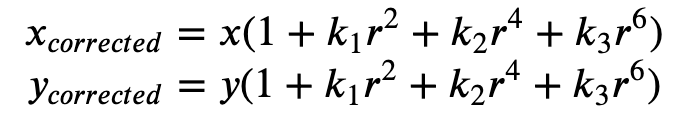
A distorção tangencial ocorre porque as lentes usadas para capturar as imagens não estão perfeitamente em paralelo em relação ao plano da imagem. Isso pode ser corrigido com a Fórmula 2.

Fórmula 2:

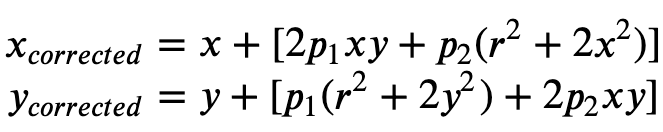
No arquivo manifesto de entrada, você pode fornecer coeficientes de distorção e o Ground Truth corrigirá a distorção das imagens. Todos os coeficientes de distorção são flutuantes.

Se a distorção já estiver corrigida nas imagens, todos os coeficientes de distorção devem ser 0 no manifesto de entrada.

A fim de reconstruir corretamente a imagem corrigida, o Ground Truth faz uma conversão de unidade das imagens com base em distâncias focais. Se uma distância focal comum for usada com determinada relação de aspecto para ambos os eixos, como 1, na fórmula superior teremos uma única distância focal. A matriz que contém esses quatro parâmetros é chamada de matriz de calibração intrínseca na câmera.

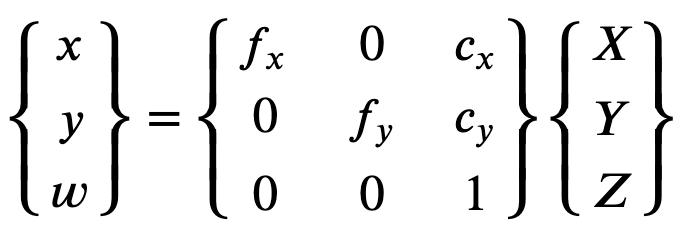
Embora os coeficientes de distorção sejam os mesmos, independentemente das resoluções de câmera usadas, eles devem ser dimensionados com a resolução atual da resolução calibrada.

Veja a seguir os valores flutuantes.

O Ground Truth usa a câmera extrínseca e a câmera intrínseca para calcular métricas de visualização, conforme mostrado no bloco de código a seguir, para transformar rótulos entre a cena 3D e imagens 2D.

def generate_view_matrix(intrinsic_matrix, extrinsic_matrix):
    intrinsic_matrix = np.c_[intrinsic_matrix, np.zeros(3)]
    view_matrix = np.matmul(intrinsic_matrix, extrinsic_matrix)
    view_matrix = np.insert(view_matrix, 2, np.array((0, 0, 0, 1)), 0)
    return view_matrix