本文属于机器翻译版本。若本译文内容与英语原文存在差异,则一律以英文原文为准。
了解坐标系和传感器融合
点云数据始终位于坐标系中。该坐标系可能是检测周围环境的车辆或设备的局部坐标系,也可能是世界坐标系。在使用 Ground Truth 3D 点云标注作业时,所有注释是使用输入数据的坐标系生成的。对于某些标注作业任务类型和功能,您必须在世界坐标系中提供数据。
在本主题中,您将了解以下内容:
-
当您需要在世界坐标系或全局参照系中提供输入数据时。
-
什么是世界坐标,以及如何将点云数据转换为世界坐标系?
-
在使用传感器融合时,如何使用传感器和摄像机外部矩阵提供姿势数据?
标注作业的坐标系要求
如果点云数据是在局部坐标系中收集的,您可以使用用于收集数据的传感器的外部矩阵将其转换为世界坐标系或全局参照系。如果无法为您的点云数据获取外部矩阵,因而无法在世界坐标系中获取点云,您可以在局部坐标系中为 3D 点云对象检测和语义分割任务类型提供点云数据。
对于对象跟踪,您必须在世界坐标系中提供点云数据。这是因为在多个帧中跟踪对象时,自主车辆本身正在世界中移动,因此,所有帧都需要一个参照点。
如果包含用于传感器融合的相机数据,则建议您在与 3D 传感器(例如 Li DAR 传感器)相同的世界坐标系中提供相机姿势。
在世界坐标系中使用点云数据
本节解释了什么是世界坐标系 (WCS)(也称为全球参考系),并说明了如何在世界坐标系中提供点云数据。
什么是世界坐标系?
WCS或全局参考系是放置车辆和传感器坐标系的固定通用坐标系。例如,如果多个点云帧由于是从两个传感器收集而位于不同的坐标系中,则WCS可以使用 a 将这些点云帧中的所有坐标转换为单个坐标系,其中所有帧都具有相同的原点,(0,0,0)。这种变换是通过使用平移向量将每个帧的原点平移到原点,然后WCS使用旋转矩阵将三个轴(通常是 x、y 和 z)向右旋转来完成的。这种刚体变换称为齐次变换。
世界坐标系在全球路径规划、定位、地图绘制和驾驶场景模拟中非常重要。Ground Truth 使用右手笛卡尔世界坐标系,例如 ISO8855
全局参照系取决于数据。有些数据集使用第一帧中的 Li DAR 位置作为原点。在这种情况下,所有帧将第一帧作为参照,并且设备方向和位置在第一帧的原点附近。例如,KITTI数据集以第一帧作为世界坐标的参考。其他数据集使用不同于原点的设备位置。
请注意,这不是GPS/IMU coordinate system, which is typically rotated by 90 degrees along the z-axis. If your point cloud data is in a GPS/IMU坐标系(例如开源 AV KITTI 数据集中的 OxTS),则需要将原点转换为世界坐标系(通常是车辆的参考坐标系)。您可以将数据乘以变换指标(旋转矩阵和平移向量)以应用这种变换。这会将数据从原始坐标系变换为全局参照坐标系。请在下一节中了解这种变换的更多信息。
将 3D 点云数据转换为 WCS
Ground Truth 假设点云数据已变换为所选的参照坐标系。例如,您可以选择传感器的参考坐标系(例如 LiDAR)作为全局参考坐标系。您也可以从不同传感器中获取点云,并将其从传感器的视图变换为车辆的参照坐标系视图。您可以使用传感器的外在矩阵(由旋转矩阵和平移向量组成)将点云数据转换为WCS或全局参考系。
平移向量和旋转矩阵可以共同构成外在矩阵,该矩阵可用于将数据从局部坐标系转换为。WCS例如,你的 Li DAR 外在矩阵可以按如下方式组成,其中R是旋转矩阵,T是平移向量:
LiDAR_extrinsic = [R T;0 0 0 1]
例如,自动驾驶KITTI数据集包括旋转矩阵和每个帧的 Li DAR 外在变换矩阵的平移向量。pykittidataset.oxts[i].T_w_imu给出了i第 n 帧的 Li DAR 外在变换,可以乘以该帧中的点将其转换为世界框架-。np.matmul(lidar_transform_matrix, points)将 Li DAR 帧中的一个点与 Li DAR 外在矩阵相乘会将其转换为世界坐标。通过将世界坐标系中的点与摄像机外部矩阵相乘,可以得出摄像机的参照系中的点坐标。
以下代码示例演示了如何将KITTI数据集中的点云帧转换为WCS.
import pykitti import numpy as np basedir = '/Users/nameofuser/kitti-data' date = '2011_09_26' drive = '0079' # The 'frames' argument is optional - default: None, which loads the whole dataset. # Calibration, timestamps, and IMU data are read automatically. # Camera and velodyne data are available via properties that create generators # when accessed, or through getter methods that provide random access. data = pykitti.raw(basedir, date, drive, frames=range(0, 50, 5)) # i is frame number i = 0 # lidar extrinsic for the ith frame lidar_extrinsic_matrix = data.oxts[i].T_w_imu # velodyne raw point cloud in lidar scanners own coordinate system points = data.get_velo(i) # transform points from lidar to global frame using lidar_extrinsic_matrix def generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix): tps = [] for point in points: transformed_points = np.matmul(lidar_extrinsic_matrix, np.array([point[0], point[1], point[2], 1], dtype=np.float32).reshape(4,1)).tolist() if len(point) > 3 and point[3] is not None: tps.append([transformed_points[0][0], transformed_points[1][0], transformed_points[2][0], point[3]]) return tps # customer transforms points from lidar to global frame using lidar_extrinsic_matrix transformed_pcl = generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix)
传感器融合
Ground Truth 支持将点云数据与最多 8 个视频摄像机输入进行传感器融合。此功能允许人工贴标者使用同步的视频帧查看 3D 点云帧 side-by-side。除了为标注提供更多视觉上下文以外,工作人员还可以通过传感器融合在 3D 场景和 2D 图像中调整注释,调整内容将投影到另一个视图中。以下视频演示了使用 Li DAR 和相机传感器融合的 3D 点云标注作业。
为了获得最佳结果,使用传感器融合时,您的点云应位于WCS. Ground Truth 使用你的传感器(例如 LiDAR)、相机和自我载具姿态信息来计算传感器融合的外在和内在矩阵。
外部矩阵
Ground Truth 使用传感器(例如 LiDAR)外部矩阵和摄像机外在矩阵和内在矩阵将物体投射到点云数据的参考帧中,以及从点云数据的参考帧投射到摄像机的参考框架。
例如,为了将标签从 3D 点云投影到摄像机图像平面,Ground Truth 会将 3D 点从 Li DAR 自己的坐标系转换为摄像机的坐标系。这通常是通过首先使用 Li DAR 外在矩阵将 3D 点从 Li DAR 自己的坐标系转换为世界坐标系(或全局参考系)来完成的。然后,Ground Truth 使用摄像机逆外部矩阵(将点从全局参照系变换为摄像机的参照系)将上一步中获得的世界坐标系中的 3D 点变换为摄像机图像平面。Li DAR 外在矩阵也可以用来将 3D 数据转换为世界坐标系。如果 3D 数据已变换为世界坐标系,则第一次变换不会对标签平移产生任何影响,标签平移仅取决于摄像机逆外部矩阵。视图矩阵用于将投影的标签可视化。要了解这些变换和视图矩阵的更多信息,请参阅Ground Truth 传感器融合变换。
Ground Truth 使用你提供的 Li DAR 和相机姿势数据来计算这些外在矩阵:heading(以四元数表示:、、和)和(qx,qyqz,)。qw position x y z对于车辆,通常通过世界坐标系中的车辆参照系描述方向和位置,它们称为自主车辆姿势。对于每个摄像机外部矩阵,您可以为该摄像机添加姿势信息。有关更多信息,请参阅 姿势。
内部矩阵
Ground Truth 使用摄像机外部矩阵和内部矩阵来计算视图指标,以便在 3D 场景和摄像机图像之间变换标签。Ground Truth 使用您提供的摄像机焦距 (fx, fy) 和光学中心坐标 (cx,cy) 来计算摄像机内部矩阵。有关更多信息,请参阅 内部矩阵和畸变。
图像畸变
图像畸变可能是由于多种原因而发生的。例如,图像可能由于桶形或鱼眼效应而发生畸变。Ground Truth 使用内部参数以及畸变系数以校正您在创建 3D 点云标注作业时提供的图像的畸变。如果已校正摄像机图像畸变,则所有畸变系数应设置为 0。
有关 Ground Truth 为校正图像畸变而执行的变换的更多信息,请参阅摄像机校准:外部矩阵、内部矩阵和畸变。
自主车辆
为了收集用于自动驾驶应用程序的数据,将从安装在车辆或自主车辆上的传感器中获取用于生成点云数据的测量值。要在 3D 场景和 2D 图像之间投影标签调整,Ground Truth 需要使用世界坐标系中的自主车辆姿势。自主车辆姿势由位置坐标和方向四元数组成。
Ground Truth 使用自主车辆姿势来计算旋转和变换矩阵。三维旋转可以表示为一系列围绕一些轴的三次旋转。理论上,跨 3D 欧几里德空间的任意三个轴就足够了。在实践中,将选择旋转轴以作为基本向量。这三次旋转需要在全局参照系(外部)中进行。Ground Truth 不支持以物体为中心的参照系(内部),该参照系附加到旋转的对象并随之旋转。为了跟踪对象,Ground Truth 需要从所有车辆行驶时所在的全局参照中进行测量。在使用 Ground Truth 3D 点云标注作业时,z 指定旋转轴(外部旋转),并且偏转欧拉角以弧度(旋转角)表示。
姿势
Ground Truth 将姿势信息用于 3D 可视化和传感器融合。您通过清单文件输入的姿势信息用于计算外部矩阵。如果您已具有外部矩阵,您可以使用该矩阵提取传感器和摄像机姿势数据。
例如,在自动驾驶KITTI数据集中,pykittidataset.oxts[i].T_w_imu给出了i第 n 帧的 Li DAR 外在变换,可以将其与点相乘以获得世界帧中的点-. matmul(lidar_transform_matrix,
points) 对于输入清单文件格式,此变换可以转换为 Li 的位置(平移向量)和标题(以四元数DAR为单位)。JSONinv(matmul(dataset.calib.T_cam0_velo,
inv(dataset.oxts[i].T_w_imu))) 可以计算第 i 帧中的 cam0 的摄像机外部变换,并将其转换为 cam0 方向和位置。
import numpy rotation = [[ 9.96714314e-01, -8.09890350e-02, 1.16333982e-03], [ 8.09967396e-02, 9.96661051e-01, -1.03090934e-02], [-3.24531964e-04, 1.03694477e-02, 9.99946183e-01]] origin= [1.71104606e+00, 5.80000039e-01, 9.43144935e-01] from scipy.spatial.transform import Rotation as R # position is the origin position = origin r = R.from_matrix(np.asarray(rotation)) # heading in WCS using scipy heading = r.as_quat() print(f"pose:{position}\nheading: {heading}")
位置
在输入清单文件中,position 指的是传感器相对于世界坐标系的位置。如果您无法将设备位置置于世界坐标系中,则可以使用带有局部坐标的 Li DAR 数据。同样,对于安装的视频摄像机,您可以在世界坐标系中指定位置和方向。对于摄像机,如果您没有位置信息,请使用 (0, 0, 0)。
以下是 position 对象中的字段:
-
x(浮点值)– 自主车辆、传感器或摄像机位置的 x 坐标(以米为单位)。 -
y(浮点值)– 自主车辆、传感器或摄像机位置的 y 坐标(以米为单位)。 -
z(浮点值)– 自主车辆、传感器或摄像机位置的 z 坐标(以米为单位)。
以下是positionJSON对象的示例:
{ "position": { "y": -152.77584902657554, "x": 311.21505956090624, "z": -10.854137529636024 } }
Heading
在输入清单文件中,heading 是一个对象,它表示设备相对于世界坐标系的方向。heading 值应以四元数表示。四元数(qx = 0, qy = 0, qz
= 0, qw = 1)。同样,对于摄像机,请以四元数形式指定方向。如果您无法获取外部摄像机校准参数,请也使用标识四元数。
heading 对象中的字段如下所示:
-
qx(浮点值)- 自主车辆、传感器或摄像机方向的 x 分量。 -
qy(浮点值)- 自主车辆、传感器或摄像机方向的 y 分量。 -
qz(浮点值)- 自主车辆、传感器或摄像机方向的 z 分量。 -
qw(浮点值)- 自主车辆、传感器或摄像机方向的 w 分量。
以下是headingJSON对象的示例:
{ "heading": { "qy": -0.7046155108831117, "qx": 0.034278837280808494, "qz": 0.7070617895701465, "qw": -0.04904659893885366 } }
要了解更多信息,请参阅 计算方向四元数和位置。
计算方向四元数和位置
Ground Truth 要求必须以四元数形式提供所有方向或方位数据。四元数
您可以从旋转矩阵或变换矩阵中计算四元数。
如果在世界坐标系中具有旋转矩阵(由轴旋转组成)和平移向量(或原点),而不是单个 4x4 刚性变换矩阵,则可以直接使用旋转矩阵和平移向量以计算四元数。scipy
import numpy rotation = [[ 9.96714314e-01, -8.09890350e-02, 1.16333982e-03], [ 8.09967396e-02, 9.96661051e-01, -1.03090934e-02], [-3.24531964e-04, 1.03694477e-02, 9.99946183e-01]] origin = [1.71104606e+00, 5.80000039e-01, 9.43144935e-01] from scipy.spatial.transform import Rotation as R # position is the origin position = origin r = R.from_matrix(np.asarray(rotation)) # heading in WCS using scipy heading = r.as_quat() print(f"position:{position}\nheading: {heading}")
3D 旋转转换器
如果您具有 4x4 外部变换矩阵,请注意,该变换矩阵采用 [R T; 0 0 0 1] 形式,其中 R 为旋转矩阵,T 为原点平移向量。这意味着,您可以按以下方式从变换矩阵中提取旋转矩阵和平移向量。
import numpy as np transformation = [[ 9.96714314e-01, -8.09890350e-02, 1.16333982e-03, 1.71104606e+00], [ 8.09967396e-02, 9.96661051e-01, -1.03090934e-02, 5.80000039e-01], [-3.24531964e-04, 1.03694477e-02, 9.99946183e-01, 9.43144935e-01], [ 0, 0, 0, 1]] transformation = np.array(transformation ) rotation = transformation[0:3,0:3] translation= transformation[0:3,3] from scipy.spatial.transform import Rotation as R # position is the origin translation position = translation r = R.from_matrix(np.asarray(rotation)) # heading in WCS using scipy heading = r.as_quat() print(f"position:{position}\nheading: {heading}")
通过自己的设置,你可以使用GPS/IMU位置和方向(纬度、经度、高度和滚动、俯仰、偏航)来计算外在变换矩阵,这些变换矩阵与 ego 载具上的 Li DAR 传感器有关。例如,您可以使用KITTI原始数据计算姿势,将 oxts 数据pose = convertOxtsToPose(oxts)转换为由 4x4 刚性变换矩阵指定的局部欧几里得姿势。然后,您可以使用世界坐标系中的参照系变换矩阵,以将该姿势变换矩阵变换为全局参照系。
struct Quaternion { double w, x, y, z; }; Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X) { // Abbreviations for the various angular functions double cy = cos(yaw * 0.5); double sy = sin(yaw * 0.5); double cp = cos(pitch * 0.5); double sp = sin(pitch * 0.5); double cr = cos(roll * 0.5); double sr = sin(roll * 0.5); Quaternion q; q.w = cr * cp * cy + sr * sp * sy; q.x = sr * cp * cy - cr * sp * sy; q.y = cr * sp * cy + sr * cp * sy; q.z = cr * cp * sy - sr * sp * cy; return q; }
Ground Truth 传感器融合变换
以下几节更详细地介绍了使用您提供的姿势数据执行的 Ground Truth 传感器融合变换。
Li DAR Etrinsic
为了在 3D Li DAR 场景之间投影到 2D 摄像机图像,Ground Truth 使用自我的车辆姿势和航向计算刚性变换投影指标。Ground Truth 执行一系列简单的旋转和平移,以计算世界坐标到 3D 平面的旋转和平移。
Ground Truth 使用方向四元数来计算旋转指标,如下所示:
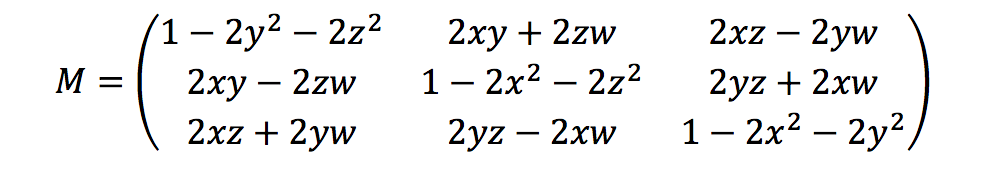
这里,[x, y, z, w]对应于headingJSON对象中的参数[qx, qy, qz, qw]。Ground Truth 以 T = [poseX, poseY, poseZ] 形式计算平移列向量。然后,外部指标就如同下面所示:
LiDAR_extrinsic = [R T;0 0 0 1]
摄像机校准:外部矩阵、内部矩阵和畸变
几何摄像机校准(也称为摄像机标定)估算图像或视频摄像机的镜头和图像传感器的参数。您可以使用这些参数校正镜头畸变,以世界单位测量对象的大小或确定摄像机在场景中的位置。摄像机参数包括内部和畸变系数。
摄像机外部矩阵
如果提供了摄像机姿势,则 Ground Truth 根据从 3D 平面到摄像机平面的刚性变换以计算摄像机外部矩阵。计算方法与用于 Li DAR Etrinsic 的方法相同,所不同的是 Ground Truth 使用摄像机姿势(position 和 heading)并计算逆外部矩阵。
camera_inverse_extrinsic = inv([Rc Tc;0 0 0 1]) #where Rc and Tc are camera pose components
内部矩阵和畸变
某些摄像机(如针孔或鱼眼摄像机)可能会导致照片严重畸变。这种畸变可以使用畸变系数和摄像机焦距来纠正。要了解更多信息,请参阅 OpenCV 文档中的使用 OpenCV 校准摄像机
Ground Truth 可以纠正两种类型的畸变:径向畸变和切向畸变。
如果光线在镜头边缘附近的弯曲程度超过光学中心,就会发生径向畸变。镜头越小,畸变越大。径向畸变以桶形或鱼眼效应的形式表现出来,Ground Truth 使用公式 1 校正这种畸变。
公式 1:
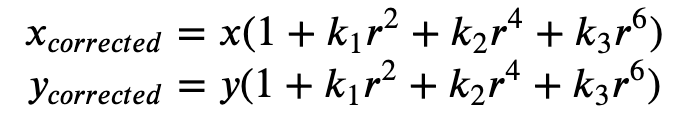
发生切向畸变是因为,用于拍摄图像的镜头未完全平行于成像平面。可以使用公式 2 校正这种畸变。
公式 2:
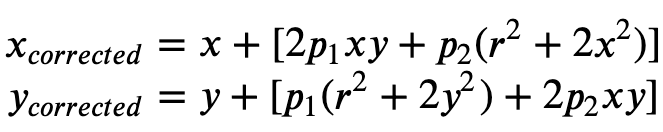
在输入清单文件中,您可以提供畸变系数,Ground Truth 将校正图像畸变。所有畸变系数均为浮点值。
-
k1、k2、k3、k4– 径向畸变系数。鱼眼和针孔摄像机型号支持。 -
p1、p2– 切向畸变系数。针孔摄像机型号支持。
如果已校正图像畸变,输入清单中的所有畸变系数应为 0。
为了正确重建校正的图像,Ground Truth 根据焦距对图像进行单位转换。如果在两个轴中将相同的焦距用于给定宽高比(例如 1),在上面的公式中,我们将具有单个焦距。包含这四个参数的矩阵称为摄像机内部校准矩阵。
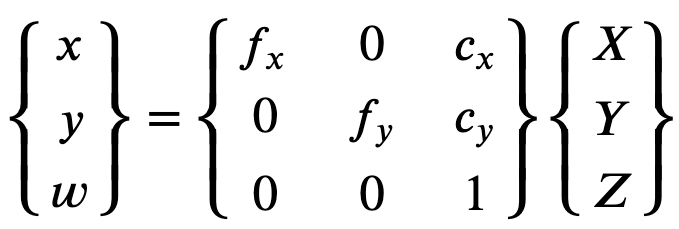
尽管畸变系数是相同的(而不管使用的摄像机分辨率如何),但应使用校准的分辨率缩放当前分辨率的系数。
以下是浮点值。
-
fx- x 方向的焦距。 -
fy- y 方向的焦距。 -
cx- 主点的 x 坐标。 -
cy- 主点的 y 坐标。
Ground Truth 使用摄像机外部和内部矩阵以计算视图指标(如以下代码块中所示),以便在 3D 场景和 2D 图像之间变换标签。
def generate_view_matrix(intrinsic_matrix, extrinsic_matrix): intrinsic_matrix = np.c_[intrinsic_matrix, np.zeros(3)] view_matrix = np.matmul(intrinsic_matrix, extrinsic_matrix) view_matrix = np.insert(view_matrix, 2, np.array((0, 0, 0, 1)), 0) return view_matrix