此頁面僅適用於使用 Vault 和 REST API 2012 年原始版本的 S3 Glacier 服務的現有客戶。
如果您要尋找封存儲存解決方案,建議您在 Amazon S3、S3 Glacier S3 Instant Retrieval、S3 Glacier Flexible Retrieval 和 S3 Glacier Deep Archive 中使用 S3 Glacier 儲存類別。若要進一步了解這些儲存選項,請參閱 Amazon S3
本文為英文版的機器翻譯版本,如內容有任何歧義或不一致之處,概以英文版為準。
下載資料時接收檢查總和
當您使用啟動任務 API 擷取封存時 (請參閱 啟動 Job (POST工作)),您可以選擇性指定擷取封存的範圍。同樣地,當您使用取得任務輸出 API 下載資料時 (請參閱 「取得任務輸出」 (GET 輸出)),您可以選擇指定各種下載資料。當您在擷取和下載封存的資料時,務必要了解這些範圍的兩個特性。擷取範圍對封存而言需要符合 MB。擷取範圍和下載範圍都必須符合樹雜湊,才能在您下載資料時接收檢查總和值。這兩種類型的範圍合規遵循的定義如下:
-
百萬位元組對齊-範圍 [StartByte, EndBytes] 是百萬位元組 (1024*1024) 對齊時StartBytes可以被 1 MB 整除,或者等於指定的歸檔結尾 (封存位元組EndBytes大小減 1)。如果有指定,啟動任務 API 中使用的範圍需要符合 MB。
-
樹哈希對齊-當且僅當建立在範圍上的樹哈希的根等同於整個存檔的樹哈希中的節點時,range [StartBytes, EndBytes] 才是樹哈希相對於存檔對齊的樹哈希值。擷取範圍和下載範圍都必須符合樹雜湊,才能接收您下載資料的檢查總和值。如需範圍範例及其與封存樹雜湊之關係的詳細資訊,請參閱 樹雜湊範例:擷取符合樹雜湊的封存範圍。
請注意,符合樹雜湊之範圍,也符合 MB。然而,符合 MB 範圍並不一定需符合樹雜湊。
以下案例描述您何時在下載封存資料接收檢查總和值:
-
如果您未在啟動任務請求中指定擷取的範圍,而且在取得任務請求中下載整個封存。
-
如果您未在啟動任務請求中指定擷取的範圍,卻在取得任務請求中指定符合樹雜湊的範圍。
-
如果您在啟動任務請求中指定符合樹雜湊的範圍,而且在取得任務請求中下載整個範圍。
-
如果您在啟動任務請求中指定符合樹雜湊的範圍,並且在取得任務請求中指定符合樹雜湊的範圍。
如果您在啟動任務請求中指定非符合樹雜湊的擷取範圍,您仍然可以取得封存資料,但在取得任務請求中下載資料時並未有任何檢查總和值傳回。
樹雜湊範例:擷取符合樹雜湊的封存範圍
假設您的保存庫中有 6.5 MB 的封存,而您想要擷取 2 MB 的封存。您如何在啟動任務請求中指定 2 MB 範圍,決定您是否會在下載資料時接收資料檢查總和值。下圖說明您可以下載的兩個用於 6.5 MB 封存的 2 MB 範圍。兩個範圍都是符合 MB,但只有一個符合樹雜湊。
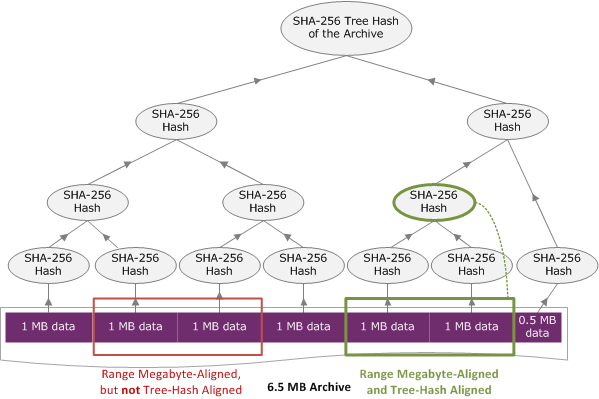
符合樹雜湊範圍規格
本節提供構成符合樹雜湊範圍的確切規格。下載封存的一部分,以及當指定擷取資料的範圍,並從擷取之資料下載的範圍時,符合樹雜湊範圍至關重要。如果這兩種範圍都符合樹雜湊,您將在下載資料時接收檢查總和資料。
範圍 [A、B] 是與封存相關的符合樹雜湊,如果且只有在新的樹雜湊建置在 [A、B] 上,且該範圍的樹雜湊根目錄等同於整個封存的樹雜湊節點。您可以查看相關內容,如 樹雜湊範例:擷取符合樹雜湊的封存範圍 圖中所示。在本節中,我們提供了適用於符合樹雜湊的規格。
考量 [P、Q] 為 N 百萬位元組 (MB) 的封存範圍查詢,而 P 和 Q 則是一 MB 的倍數。請注意,實際包含範圍是 [P MB、Q MB – 1 個位元組],但為簡單化,我們會將它顯示為 [P、Q]。在這些考量下,然後
-
如果 P 是奇數,僅有一個可能的符合樹雜湊範圍 - 就是[P、P + 1 MB]。
-
如果 P 是偶數,而 k 是最大數,其中 P 可以編寫為 2k * X,則最多有 k 個符合樹雜湊範圍以 P 開頭。X 是大於 0 的整數。符合樹雜湊的範圍落在下列類別:
-
對於每個 i,其中 (0 <= i <= k) 而且 P + 2i < N,然後 [P、Q + 2i] 是符合樹雜湊的範圍。
-
P = 0 是特殊情況,其中 A = 2[lgN]*0
-