互動旋轉鏈安排互動駕駛欄位 AHS 程式在本機模擬器上執行分析模擬器結果在 QuEraAquila 上執行 QPU 分析QPU結果後續步驟

您好AHS：執行您的第一個類比 Hamiltonian 模擬

本節提供執行第一個類比 Hamiltonian 模擬的相關資訊。

在本節中：

互動旋轉鏈
安排
互動
駕駛欄位
AHS 程式
在本機模擬器上執行
分析模擬器結果
在 QuEraAquila 上執行 QPU
分析QPU結果
後續步驟

互動旋轉鏈

如需許多互動粒子系統的正式範例，讓我們考慮一個八次旋轉的環（每個旋轉環都可以是「向上」∣↑⟩ 和「向下」∣↓⟩ 狀態）。雖然很小，但此模型系統已展現一些自然產生磁性材料的有趣現象。在此範例中，我們將示範如何準備所謂的抗鐵磁順序，其中連續旋轉指向相反方向。

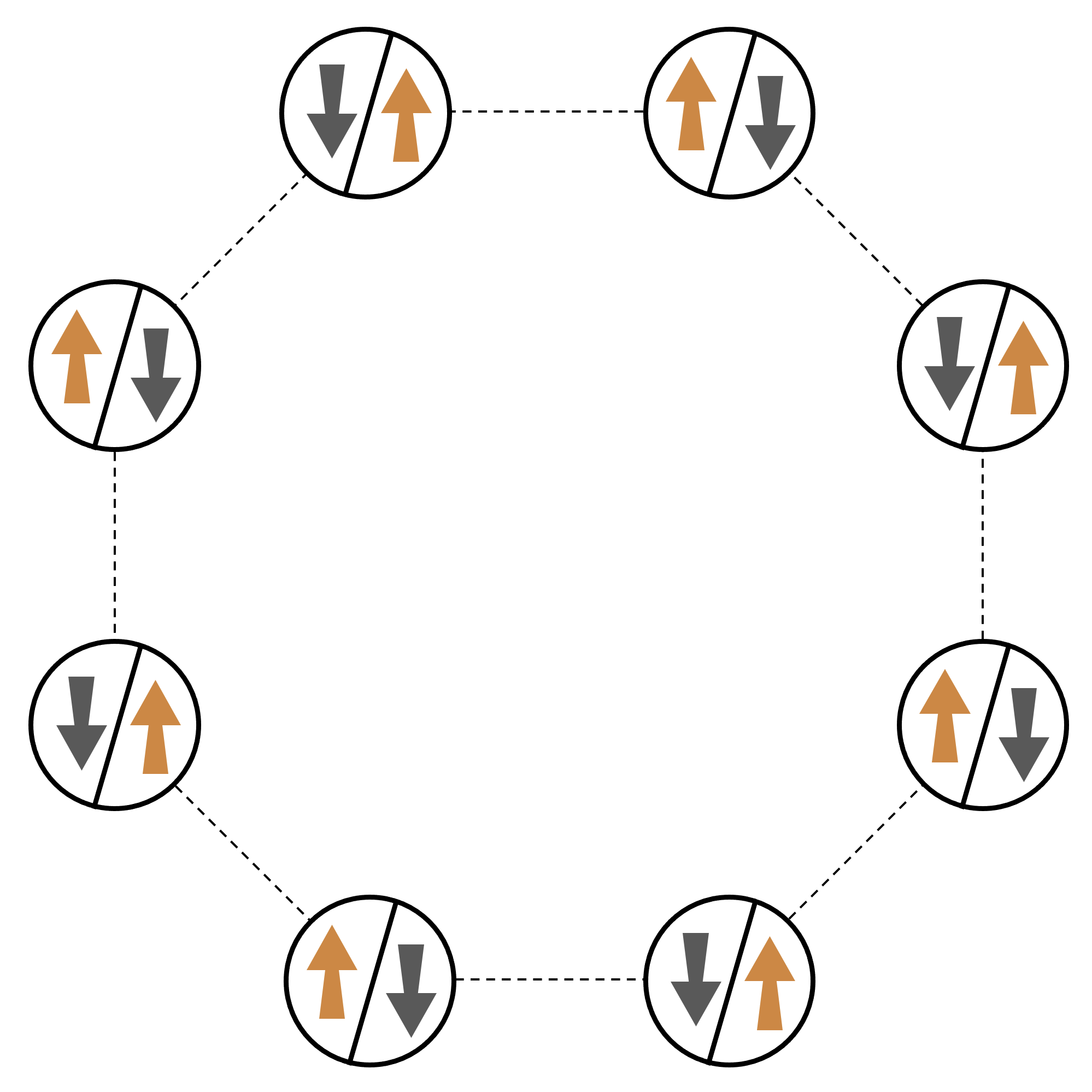
安排

我們將使用一個中性原子來代表每次旋轉，而「向上」和「向下」旋轉狀態將分別以激磁的 Rydberg 狀態和原子的接地狀態進行編碼。首先，我們建立 2 天排列。我們可以使用下列程式碼來編寫上述旋轉環的程式。

先決條件：您需要 pip 安裝 Braket SDK。（如果您使用的是 Braket 託管筆記本執行個體，SDK則會預先安裝筆記本。) 若要重現圖，您也需要使用 shell 命令單獨安裝 matplotlibpip install matplotlib。


import numpy as np
   import matplotlib.pyplot as plt  # required for plotting
   
   from braket.ahs.atom_arrangement import AtomArrangement
   
   a = 5.7e-6  # nearest-neighbor separation (in meters)
   
   register = AtomArrangement()
   register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
   register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
   register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

我們也可以使用繪製


fig, ax = plt.subplots(1, 1, figsize=(7,7))
   xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
   ax.plot(xs, ys, 'r.', ms=15)
   for idx, (x, y) in enumerate(zip(xs, ys)):
       ax.text(x, y, f" {idx}", fontsize=12)
   plt.show()  # this will show the plot below in an ipython or jupyter session

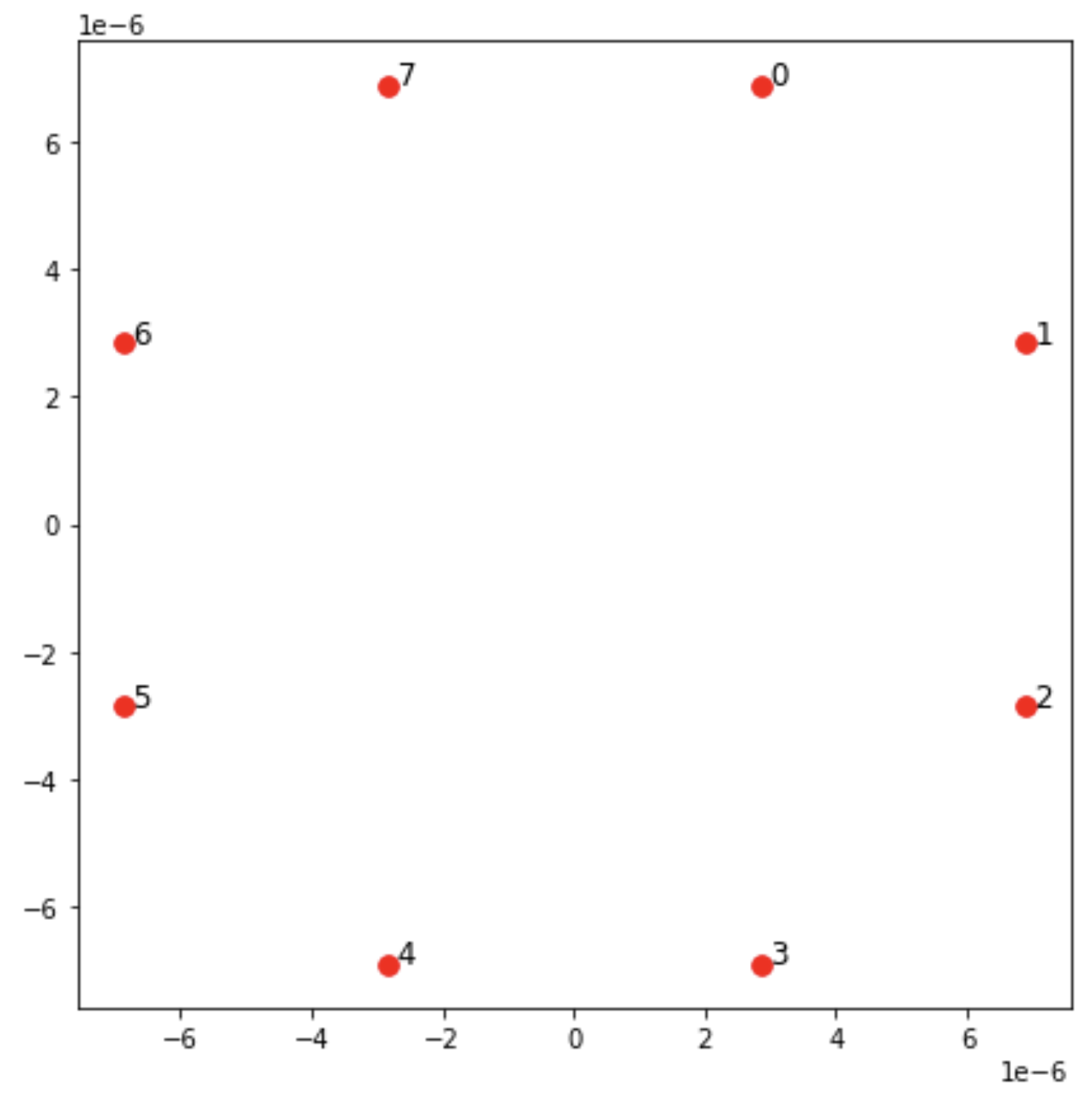
互動

若要準備抗鐵磁階段，我們需要在鄰近旋轉之間觸發互動。我們對此使用 van der Waals 互動，這是由中性原子裝置（例如 Aquila 裝置來自 QuEra)。使用旋轉代表法，此互動的漢密爾頓語詞彙可以用總和表示，超過所有旋轉對 (j，k)。

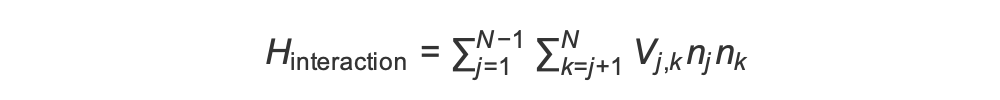
在此，nj =_j_j∣↑⟩⟨↑∣ 是運算子，只有在旋轉 j 處於「上升」狀態時，才會取得 1 的值，否則為 0。強度為 V_j,k=C₆/(d_j,k)⁶，其中 ₆Cis 是固定係數，而 dis _j,k是旋轉 j 和 k 之間的歐克里代斯距離。此互動術語的立即效果是，任何旋轉 j 和旋轉 k 都為「向上」的狀態都具有提升的能量（以 V 量表示_j,k)。透過仔細設計AHS程式的其餘部分，此互動將防止相鄰旋轉同時處於「上」狀態，這是一種通常稱為「Rydberg 封鎖」的效果。

駕駛欄位

在AHS程式開始時，所有旋轉（預設）都會以「向下」狀態開始，處於所謂的鐵磁階段。密切關注準備抗鐵磁階段的目標，我們會指定時間相依的一致駕駛欄位，可將旋轉從此狀態平順地轉換為「上升」狀態的許多身體狀態。對應的 Hamiltonian 可以寫入為

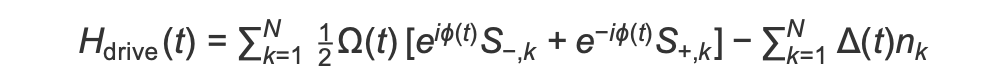
其中 Ω(t)、φ(t)、Δ(t) 是時間相依性、全域振幅（也稱為 Rabi 頻率)、階段和調整影響所有旋轉的驅動欄位。此處的 S_−,k=_k_k∣↓⟩⟨↑∣和 S_+,k=(S_−,k)^†=_k_k∣↑⟩⟨↓∣ 分別是旋轉 k 的下降和提高運算子，而 n_k=_k_k∣��↑⟩⟨↑∣ 與之前相同。駕駛欄位的 Ω 部分會同時聯結所有旋轉的「向下」和「向上」狀態，而 Δ 部分則控制「向上」狀態的能源獎勵。

若要程式設計從鐵磁階段順利轉換至抗鐵磁階段，請使用下列程式碼指定驅動欄位。


from braket.timings.time_series import TimeSeries
   from braket.ahs.driving_field import DrivingField
   
   # smooth transition from "down" to "up" state
   time_max = 4e-6  # seconds
   time_ramp = 1e-7  # seconds
   omega_max = 6300000.0  # rad / sec
   delta_start = -5 * omega_max
   delta_end = 5 * omega_max
   
   omega = TimeSeries()
   omega.put(0.0, 0.0)
   omega.put(time_ramp, omega_max)
   omega.put(time_max - time_ramp, omega_max)
   omega.put(time_max, 0.0)
   
   delta = TimeSeries()
   delta.put(0.0, delta_start)
   delta.put(time_ramp, delta_start)
   delta.put(time_max - time_ramp, delta_end)
   delta.put(time_max, delta_end)
   
   phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)
   
   drive = DrivingField(
       amplitude=omega,
       phase=phi,
       detuning=delta
   )

我們可以使用以下指令碼視覺化駕駛欄位的時間序列。


fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)
   
   ax = axes[0]
   time_series = drive.amplitude.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Omega [rad/s]')
   
   ax = axes[1]
   time_series = drive.detuning.time_series
   ax.plot(time_series.times(), time_series.values(), '.-');
   ax.grid()
   ax.set_ylabel('Delta [rad/s]')
   
   ax = axes[2]
   time_series = drive.phase.time_series
   # Note: time series of phase is understood as a piecewise constant function
   ax.step(time_series.times(), time_series.values(), '.-', where='post');
   ax.set_ylabel('phi [rad]')
   ax.grid()
   ax.set_xlabel('time [s]')
   
   plt.show()  # this will show the plot below in an ipython or jupyter session

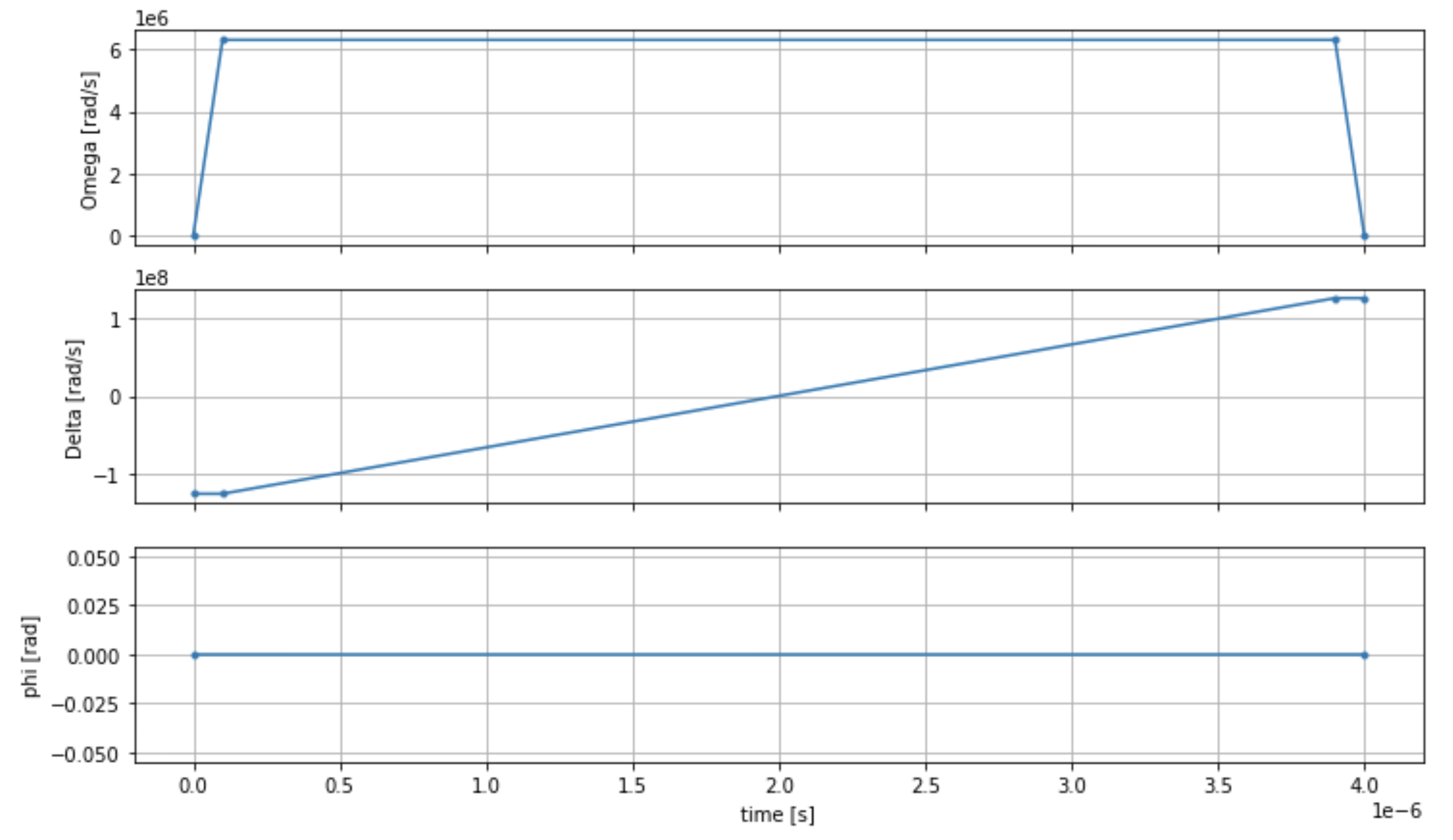
顯示隨時間變化的 phi、delta 和 Omega 的三個圖表。頂端子圖表會顯示成長至剛好超過 6 rads/s，並會保留 4 秒，直到其降回 0。中間子圖表描述衍生產品的相關線性增長，底部子圖表描述接近零的扁平線。

AHS 程式

註冊、駕駛欄位（和隱含 van der Waals 互動）組成了類比漢密爾頓模擬程式 ahs_program。


from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation
   
   ahs_program = AnalogHamiltonianSimulation(
       register=register,
       hamiltonian=drive
   )

在本機模擬器上執行

由於此範例很小（少於 15 次旋轉），在 AHS相容的上執行之前QPU，我們可以在隨 Braket 提供的本機AHS模擬器上執行SDK。由於 Braket 可免費使用本機模擬器SDK，因此最佳實務是確保程式碼可以正確執行。

在這裡，我們可以將鏡頭數量設定為高值（例如 100 萬），因為本機模擬器會追蹤量子狀態的時間演變，並從最終狀態中提取範例；因此，增加鏡頭數量，同時僅稍微增加總執行時間。


from braket.devices import LocalSimulator
   device = LocalSimulator("braket_ahs")
   
   result_simulator = device.run(
       ahs_program,
       shots=1_000_000
   ).result()  # takes about 5 seconds

分析模擬器結果

我們可以將拍攝結果彙總為下列函數，以推斷每次旋轉的狀態（可能是「d」表示「down」、「u」表示「up」或「e」表示空白網站），並計算每個組態在拍攝中發生的次數。


from collections import Counter
   
   def get_counts(result):
       """Aggregate state counts from AHS shot results
   
       A count of strings (of length = # of spins) are returned, where
       each character denotes the state of a spin (site):
          e: empty site
          u: up state spin
          d: down state spin
   
       Args:
          result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)
   
       Returns
           dict: number of times each state configuration is measured
   
       """
       state_counts = Counter()
       states = ['e', 'u', 'd']
       for shot in result.measurements:
           pre = shot.pre_sequence
           post = shot.post_sequence
           state_idx = np.array(pre) * (1 + np.array(post))
           state = "".join(map(lambda s_idx: states[s_idx], state_idx))
           state_counts.update((state,))
       return dict(state_counts)
   
   counts_simulator = get_counts(result_simulator)  # takes about 5 seconds
   print(counts_simulator)


{'udududud': 330944, 'dudududu': 329576, 'dududdud': 38033, ...}

counts 以下是字典，可計算跨鏡頭觀察每個狀態組態的次數。我們也可以使用下列程式碼將它們視覺化。


from collections import Counter
   
   def has_neighboring_up_states(state):
       if 'uu' in state:
           return True
       if state[0] == 'u' and state[-1] == 'u':
           return True
       return False
   
   def number_of_up_states(state):
       return Counter(state)['u']
   
   def plot_counts(counts):
       non_blockaded = []
       blockaded = []
       for state, count in counts.items():
           if not has_neighboring_up_states(state):
               collection = non_blockaded
           else:
               collection = blockaded
           collection.append((state, count, number_of_up_states(state)))
   
       blockaded.sort(key=lambda _: _[1], reverse=True)
       non_blockaded.sort(key=lambda _: _[1], reverse=True)
   
       for configurations, name in zip((non_blockaded,
                                       blockaded),
                                       ('no neighboring "up" states',
                                       'some neighboring "up" states')):
           plt.figure(figsize=(14, 3))
           plt.bar(range(len(configurations)), [item[1] for item in configurations])
           plt.xticks(range(len(configurations)))
           plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
           plt.ylabel('shots')
           plt.grid(axis='y')
           plt.title(f'{name} configurations')
           plt.show()
   
   plot_counts(counts_simulator)

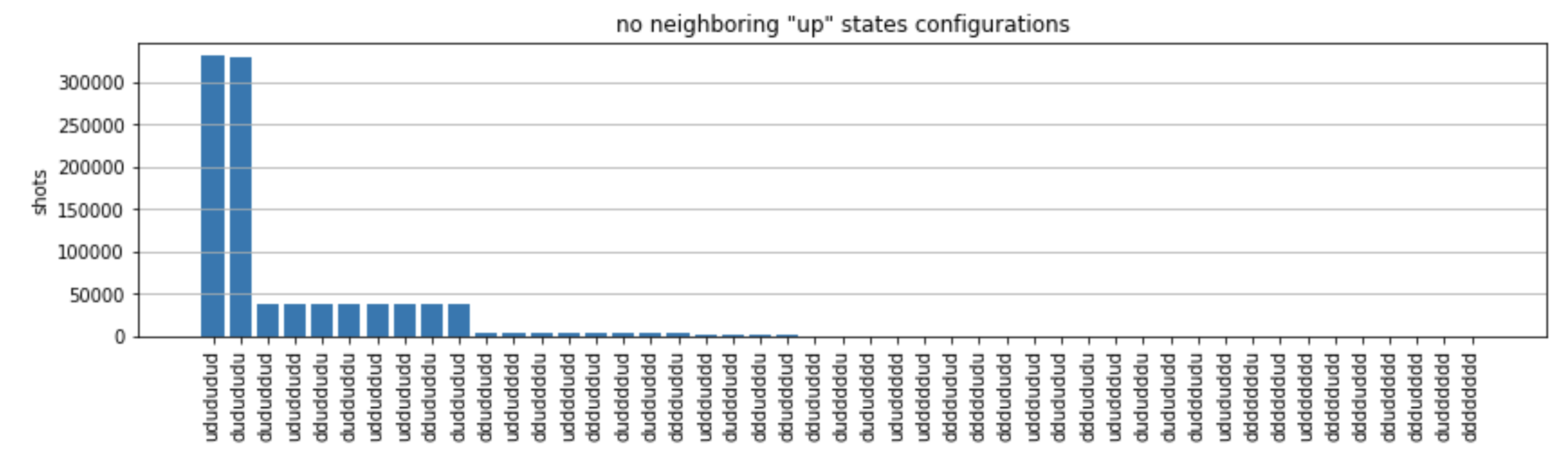
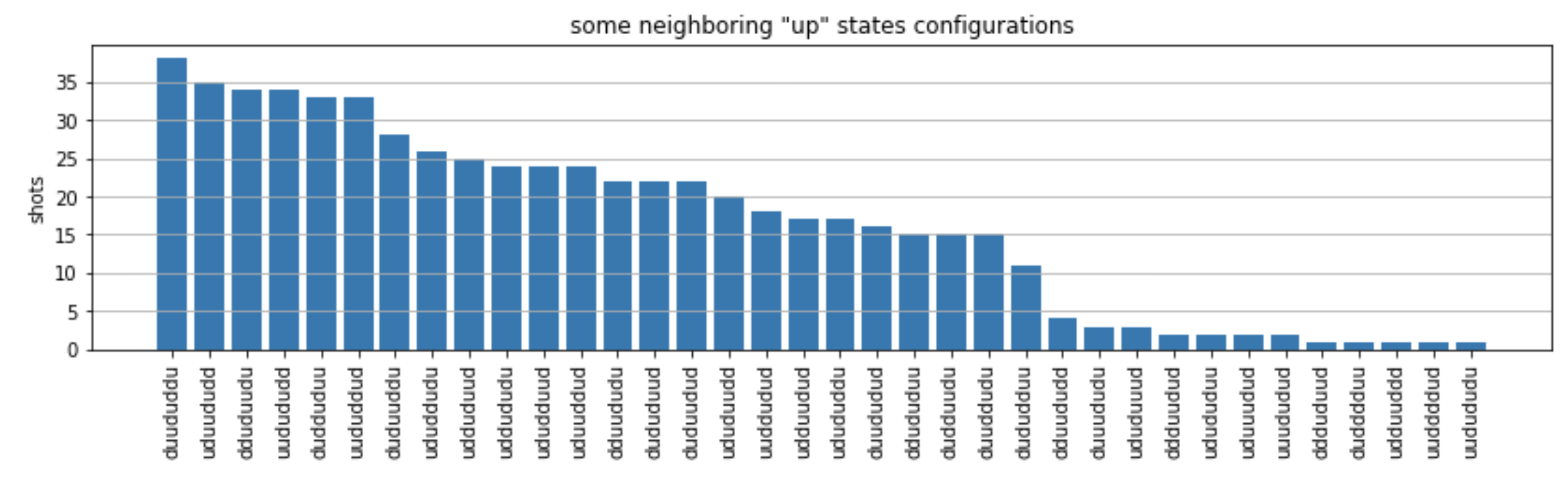
從圖中，我們可以讀取下列觀察，確認我們已成功準備抗鐵磁階段。

一般而言，非封鎖狀態（其中沒有兩個相鄰旋轉處於「上」狀態）比至少有一個相鄰旋轉處於「上」狀態的狀態更為常見。
一般而言，除非組態遭到封鎖，否則具有更多 "up" 引數的狀態是較有利的。
最常見的狀態實際上是完美的抗鐵磁狀態 "dudududu"和 "udududud"。
第二個最常見的狀態是只有 3 個連續間隔為 1、2、2 的「向上」激發。這顯示 van der Waals 互動也會對最近鄰里產生影響（雖然小得多）。

在 QuEraAquila 上執行 QPU

先決條件：除了 pip 安裝 Braket 之外SDK，如果您是 Amazon Braket 的新手，請確定您已完成必要的入門步驟。

注意

如果您使用的是 Braket 託管筆記本執行個體，則 Braket SDK會預先安裝執行個體。

安裝所有相依性後，我們可以連線至 Aquila QPU.


from braket.aws import AwsDevice
   
   aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

讓我們的AHS程式適用於 QuEra 機器，我們需要將所有值四捨五入，以符合允許的精確度層級 Aquila QPU。（這些要求由名稱中具有「解析」的裝置參數所管理。我們可以透過在筆記本aquila_qpu.properties.dict()中執行來查看它們。如需 Aquila 功能和需求的詳細資訊，請參閱 Aquila 筆記本簡介。) 我們可以呼叫 discretize方法來執行此操作。


discretized_ahs_program = ahs_program.discretize(aquila_qpu)

現在，我們可以在上執行程式（現在只執行 100 個鏡頭） Aquila QPU.

注意

在上執行此程式 Aquila 處理器會產生費用。Amazon Braket SDK包含成本追蹤器，可讓客戶設定成本限制，並近乎即時地追蹤成本。


task = aquila_qpu.run(discretized_ahs_program, shots=100)
   
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")


task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: CREATED

由於量子任務可能需要多長時間才能執行的很大差異（取決於可用性時段和QPU使用率），建議您記下量子任務 ARN，以便稍後使用下列程式碼片段來檢查其狀態。


# Optionally, in a new python session
   
   from braket.aws import AwsQuantumTask
   
   SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"
   
   task = AwsQuantumTask(arn=SAVED_TASK_ARN)
   metadata = task.metadata()
   task_arn = metadata['quantumTaskArn']
   task_status = metadata['status']
   
   print(f"ARN: {task_arn}")
   print(f"status: {task_status}")


*[Output]*
   task ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
   task status: COMPLETED

一旦狀態為 COMPLETED（也可以從 Amazon Braket 主控台的量子任務頁面檢查），我們可以使用下列方式查詢結果：


result_aquila = task.result()

分析QPU結果

使用與之前相同的get_counts函數，我們可以計算計數：


counts_aquila = get_counts(result_aquila)
   print(counts_aquila)


*[Output]*
   {'udududud': 24, 'dudududu': 17, 'dududdud': 3, ...}

並使用繪製它們plot_counts：


plot_counts(counts_aquila)

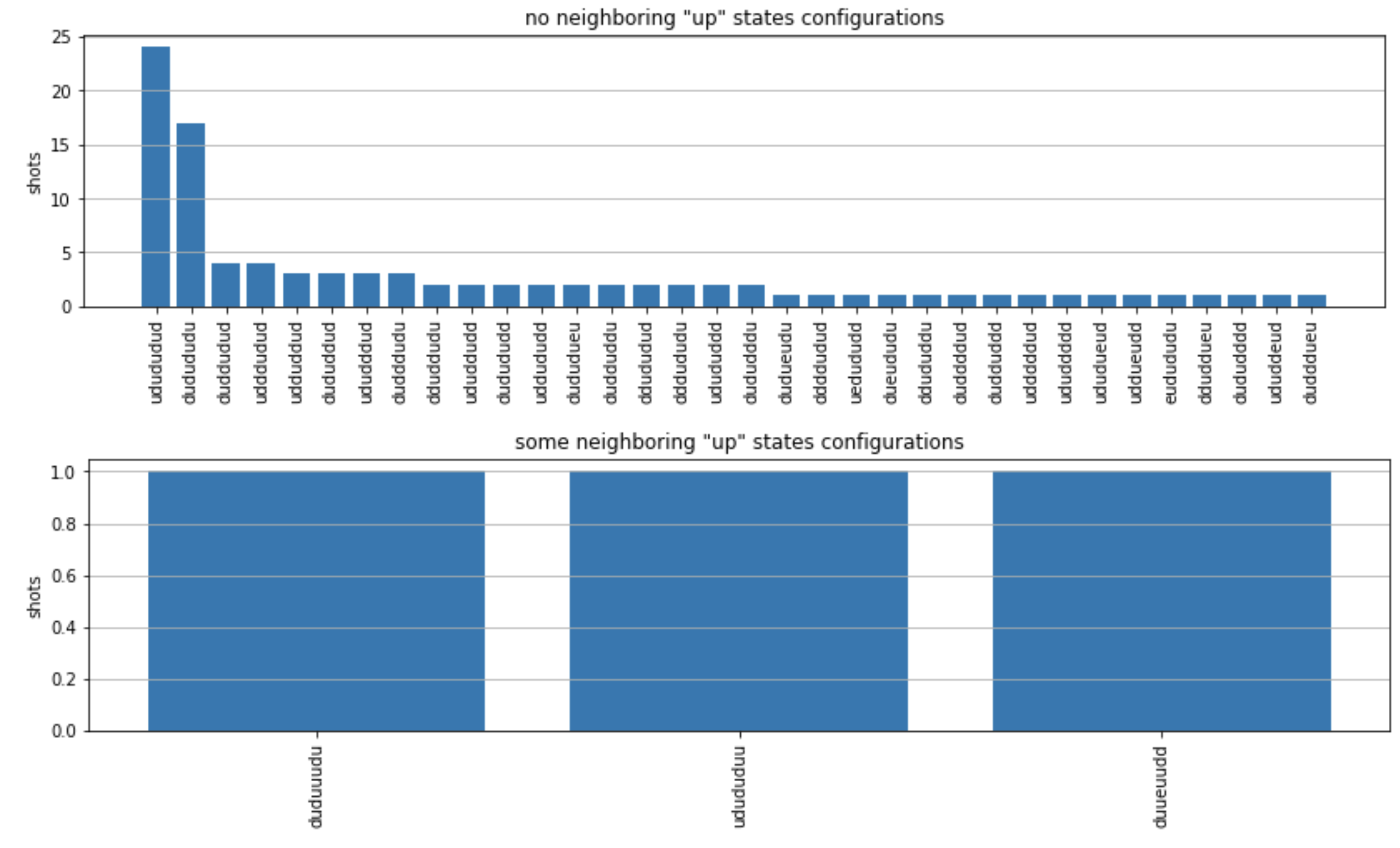
請注意，一小部分的鏡頭具有空的網站（以 “e” 標記）。這是因為的每個原子準備瑕疵為 1-2% Aquila QPU。除此之外，由於拍攝次數較少，結果與模擬在預期的統計波動內相符。

後續步驟

恭喜，您現在已使用本機模擬器和，在 Amazon Braket AHS 上執行第一個AHS工作負載 Aquila QPU.

若要進一步了解 Rydberg 物理、Analog Hamiltonian Simulation 和 Aquila 裝置，請參閱我們的筆記本範例。

您的瀏覽器已停用或無法使用 Javascript。

您必須啟用 Javascript，才能使用 AWS 文件。請參閱您的瀏覽器說明頁以取得說明。

文件慣用形式

（進階）類比漢密爾頓模擬

使用 QuEra Aquila 提交類比程式