작동 PCA 원리 - Amazon SageMaker
모드 1: Regular모드 2: Randomized

기계 번역으로 제공되는 번역입니다. 제공된 번역과 원본 영어의 내용이 상충하는 경우에는 영어 버전이 우선합니다.

작동 PCA 원리

주성분 분석 (PCA) 은 가능한 많은 정보를 유지하면서 데이터셋 내의 차원 (특징 수) 을 줄이는 학습 알고리즘입니다.

PCA구성 요소라고 하는 새로운 특징 집합을 찾아 차원을 줄입니다. 구성 요소는 원래 특징과 합성되지만 서로 상관관계가 없습니다. 첫 번째 성분은 데이터에서 가능성이 가장 큰 변수를 처리하고, 두 번째 성분은 두 번째로 큰 변수를 처리합니다.

비지도 차원 절감 알고리즘입니다. 비지도 학습에서 훈련 데이터 세트의 객체와 연결될 수 있는 레이블은 사용되지 않습니다.

각 차원 1 * d에 행 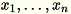x_1,…,x_n 이 있는 매트릭스 입력을 감안할 때 데이터는 행의 미니 배치로 분할되고 훈련 노드(작업자) 간에 분산됩니다. 각 작업자는 데이터의 요약을 컴퓨팅합니다. 각 작업자의 요약은 컴퓨팅 종료 시 단일 해결책으로 통합됩니다.

모드

Amazon SageMaker PCA 알고리즘은 상황에 따라 두 가지 모드 중 하나를 사용하여 이러한 요약을 계산합니다.

  • regular: 희소 데이터와 적당한 수의 관측치 및 특징이 포함된 데이터 세트.

  • randomized: 많은 수의 관측치 및 특징이 포함된 데이터 세트. 이 모드는 근사치 알고리즘을 사용합니다.

알고리즘의 마지막 단계로 통합된 해결책에 단수 값 분해를 수행하면 주성분이 파생됩니다.

모드 1: Regular

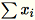작업자가 Equation in text-form: \sum x_i^T x_i 및 Equation in text-form: \sum x_i 둘 다를 공동으로 컴퓨팅합니다.

참고

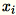Equation in text-form: x_i 가 1 * d 행 벡터가 아니기 때문에 Equation in text-form: x_i^T x_i 는 (스칼라가 아니라) 매트릭스입니다. 코드 내 행 벡터를 사용하면 효율적인 캐싱을 얻을 수 있습니다.

공분산 매트릭스는 Equation in text-form: \sum x_i^T x_i - (1/n) (\sum x_i)^T \sum x_i 및 모델의 최상위 num_components 단수 벡터로 계산됩니다.

참고

subtract_mean이 False인 경우 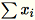Equation in text-form: \sum x_i 계산 및 빼기를 피합니다.

벡터의 d 차원이 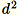Equation in text-form: d^2 이 메모리에 맞을 수 있도록 충분히 작은 경우 이 알고리즘을 사용합니다.

모드 2: Randomized

입력 데이터 세트의 특징 수가 큰 경우 메서드를 사용하여 공분산 지표의 근사치를 계산합니다. 모든 미니 배치에서 차원 b * d의 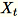Equation in text-form: X_t 의 경우 각 미니 배치를 곱한 (num_components + extra_components) * b 매트릭스를 무작위로 초기화하여 (num_components + extra_components) * d 매트릭스를 생성합니다. 이러한 행렬의 합계는 워커에 의해 계산되며 서버는 최종 SVD 행렬에서 작업을 수행합니다. (num_components + extra_components) * d 최상위 num_components 단수 벡터는 입력 매트릭스의 최상위 단수 벡터의 근사치입니다.

Equation in text-form: \ell = num_components + extra_components를 허용합니다. 차원 b * d의 미니 배치 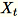Equation in text-form: X_t 를 감안해 작업자는 차원 Equation in text-form: \ell * b 의 임의 매트릭스 Equation in text-form: H_t 를 가져옵니다. 환경에서 a GPU or 또는 차원 크기를 사용하는지 여부에 따라 행렬은 각 항목이 있는 임의 부호 행렬이 +-1 되거나 a FJLT(Johnson Lindenstrauss 고속 변환, 자세한 내용은 FJLT변환 CPU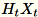 및 후속 문서 참조) 가 됩니다. 그런 다음 작업자는 Equation in text-form: H_t X_t 를 계산하고 Equation in text-form: B = \sum H_t X_t 을 보관합니다. 또한 작업자는 Equation in text-form: H_1,..,H_T (T: 미니 배치의 총 수) 열의 합계인 Equation in text-form: h^T 및 모든 입력 행의 합계인 s를 유지합니다. 전체 데이터 샤드를 처리한 이후 작업자는 서버 B, h, s 및 n을 전송합니다(입력 행의 수).

서버에 대한 여러 입력은 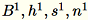Equation in text-form: B^1, h^1, s^1, n^1,… 으로 나타납니다. 서버는 B, h, s, n(각 입력의 합계)을 계산합니다. 그런 다음 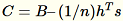Equation in text-form: C = B – (1/n) h^T s 를 계산하고 단수 값 분해를 찾습니다. 최상위 단수 벡터 및 단수 값인 C는 문제에 대한 근사치 해결책으로 사용됩니다.