如何PCA工作 - Amazon SageMaker
模式 1：一般模式 2：隨機

本文為英文版的機器翻譯版本，如內容有任何歧義或不一致之處，概以英文版為準。

如何PCA工作

主要元件分析 (PCA) 是一種學習演算法，可減少資料集內的維度 (特徵數目)，同時仍保留盡可能多的資訊。

PCA透過尋找稱為元件的新特徵集來降低標註性，這些特徵是原始特徵的複合體，但彼此不相關。第一個元件說明資料中最有可能出現的變異、第二個元件中次有可能出現的變異，以此類推。

它是無人監管的維數降低演算法。在未受監督的學習情況下，標籤可能會與訓練資料集內未使用的物件建立關聯。

指定矩陣輸入，其中包含了列 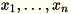x_1,…,x_n ，每個維度都是 1 * d，則資料會分割成列的迷你批次，並分散至訓練節點 (工作者)。每個工作者接著會計算資料的總和。不同工作者的摘要接著會彙整至位於運算尾端的單一解法。

模式

Amazon SageMaker PCA 演算法會根據情況，使用兩種模式中的任何一種來計算這些摘要：

  • 一般：針對含有稀疏資料的資料集以及中等數量的觀察與特徵。

  • 隨機：針對含有大量觀察與特徵的資料集。此模式使用近似值演算法。

做為演算法的最後一個步驟，它會在彙整的解法上執行單一值分解，接著主要成分會從此衍生。

模式 1：一般

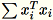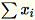工作者會共同運算 Equation in text-form: \sum x_i^T x_i 和 Equation in text-form: \sum x_i 。

注意

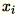由於 Equation in text-form: x_i 是 1 * d 列向量，因此 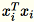Equation in text-form: x_i^T x_i 是一個矩陣 (不是純量)。在程式碼中使用行向量可讓我們獲得有效率的快取。

共變異數矩陣會運算為 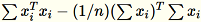Equation in text-form: \sum x_i^T x_i - (1/n) (\sum x_i)^T \sum x_i ，而其位於最前面的 num_components 個單一向量會組成模型。

注意

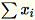若 subtract_mean 是 False，我們會避免運算及減去 Equation in text-form: \sum x_i 。

當向量的維度 d 尺寸夠小，請使用此演算法使 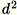Equation in text-form: d^2 能容納在記憶體中。

模式 2：隨機

在輸入資料集內的功能數量較多時，我們使用一種方法來逼近共變異數指標。針對每個維度 b * d 的迷你批次 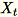Equation in text-form: X_t ，我們會隨機初始化一個 (num_components + extra_components) * b 矩陣，讓我們能夠乘以每個迷你批次，來建立一個 (num_components + extra_components) * d 矩陣。這些矩陣的總和由 Worker 計算，而伺服器會在最終(num_components + extra_components) * d矩陣SVD上執行。其中的右上方 num_components 單一向量為輸入矩陣的頂端單一維度估算值。

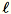
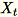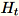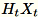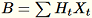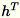使 Equation in text-form: \ell = num_components + extra_components。指定維度為 b * d 的迷你批次 Equation in text-form: X_t ，工作者會抽取一個維度為 Equation in text-form: \ell * b 的隨機矩陣 Equation in text-form: H_t 。根據環境是否使用GPU或CPU和尺寸大小，矩陣可以是每個條目所在的隨機符號矩陣+-1或一個 FJLT（快速 Johnson Lindenstrauss 轉換；有關信息，請參閱FJLT轉換和後續論文）。工作者接著會運算 Equation in text-form: H_t X_t ，並保持 Equation in text-form: B = \sum H_t X_t 。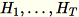工作者也會保持 Equation in text-form: h^T ，即 Equation in text-form: H_1,..,H_T (其中 T 是迷你批次的總數) 欄的總和，以及 s (所有輸入列的總和)。在處理整個資料碎片後，工作者會傳送 B、h、s 以及 n 給伺服器 (輸入行數量)。

將對伺服器的不同輸入表示為 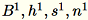Equation in text-form: B^1, h^1, s^1, n^1,… 。伺服器會運算 B、h、s、n，即個別輸入的總和。它接著會運算 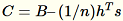Equation in text-form: C = B – (1/n) h^T s ，然後尋找其單一值的分解。使用 C 的右上單一向量與單一值做為對問題的約略解法。