本文為英文版的機器翻譯版本,如內容有任何歧義或不一致之處,概以英文版為準。
RCF 運作方式
Amazon SageMaker Random Cut Forest (RCF) 是一種無監督演算法,用於偵測資料集內的異常資料點。這些觀測到的結果,和具有良好結構或規律的資料不一致。異常情況可能會表現為時間序列資料中的意外峰值、週期性的中斷,或是無法歸類的資料點。這些異常易於辨識,因為在圖中檢視時,經常能夠明顯地區分出異常項目和 “一般” 資料。在資料集中包含這些異常項目,將會大幅提高機器學習任務的複雜度,因為 “一般” 的資料通常可以透過簡單的模型描述。
RCF 演算法背後的主要概念是建立樹系,其中每個樹狀目錄都是使用訓練資料範例的分割區取得。例如,首先會決定輸入資料的隨機樣本。然後,會根據森林中的樹狀結構數目來分割隨機樣本。接著會讓每個樹狀結構獲得此等分割區,並將這些點的子集整編為 k-d 樹。指派給資料點的異常分數,其定義為將該點加入樹狀結構時,此樹狀結構複雜度的預期變化;此等分數大致與樹狀結構中所產生的點深度成反比。隨機切割森林演算法會藉由計算出每個組成樹的平均分數,並根據樣本大小來擴充結果,以指派異常分數。RCF 演算法是以參考 【1】 中所述的演算法為基礎。
隨機抽樣資料
RCF 演算法的第一個步驟是取得訓練資料的隨機範例。特別是,假設我們希望從
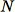 個總資料點中,抽取大小為
個總資料點中,抽取大小為
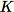 的樣本。若訓練資料夠小,即可使用整個資料集,並且我們可以從此資料集隨機抽取
的樣本。若訓練資料夠小,即可使用整個資料集,並且我們可以從此資料集隨機抽取
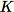 個元素。不過,訓練資料的大小經常會過大,而無法一次納入,因此這個方法並不可行。我們會改而採用稱為蓄水池取樣的技術。
個元素。不過,訓練資料的大小經常會過大,而無法一次納入,因此這個方法並不可行。我們會改而採用稱為蓄水池取樣的技術。
Reservoir sampling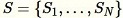 ,其中資料集內的元素只能一次觀察一個,或是以批次進行觀察。事實上,即使
,其中資料集內的元素只能一次觀察一個,或是以批次進行觀察。事實上,即使
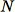 不是已知的先驗,reservoir sampling 也能運作。若只請求一個樣本 (例如當
不是已知的先驗,reservoir sampling 也能運作。若只請求一個樣本 (例如當
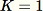 時),則演算法會如下:
時),則演算法會如下:
演算法:水塘抽樣
-
輸入:資料集或資料串流
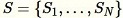
-
將隨機樣本初始化
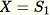
-
針對每個觀察的樣本
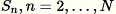 :
:-
選擇均勻隨機數
![Equation in text-form: \xi \in [0,1]](images/rcf6.jpg)
-
如果
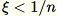
-
設定
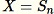
-
-
-
傳回
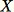
此演算法會選取一個隨機樣本,例如針對所有
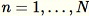 的
的
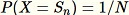 。當
。當
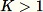 時,演算法會更複雜。此外,放回和不放回的隨機抽樣法之間,必須明確的區分。RCF 根據 【2】 中描述的演算法,在不取代訓練資料的情況下執行增強型儲存貯體取樣。
時,演算法會更複雜。此外,放回和不放回的隨機抽樣法之間,必須明確的區分。RCF 根據 【2】 中描述的演算法,在不取代訓練資料的情況下執行增強型儲存貯體取樣。
訓練RCF模型和產生推論
中的下一步RCF是使用隨機資料範例建構隨機剪切的樹系。首先,會將樣本分割為多個同等大小的分割區,其數量等於森林中樹狀結構的數量。然後,將每個分割區傳送到個別的樹狀結構。樹狀結構會藉由將資料域分割為具有邊框的方塊,來將樹其分割區以遞歸的方式整編為二元樹。
這個程序最好是透過範例說明。假設將下列的 2D 資料集分派給樹狀結構。對應的樹狀結構會從根節點起始:
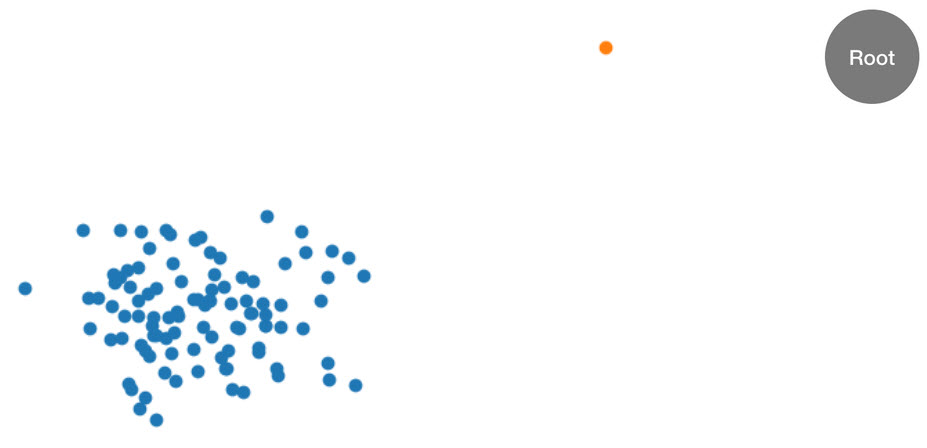
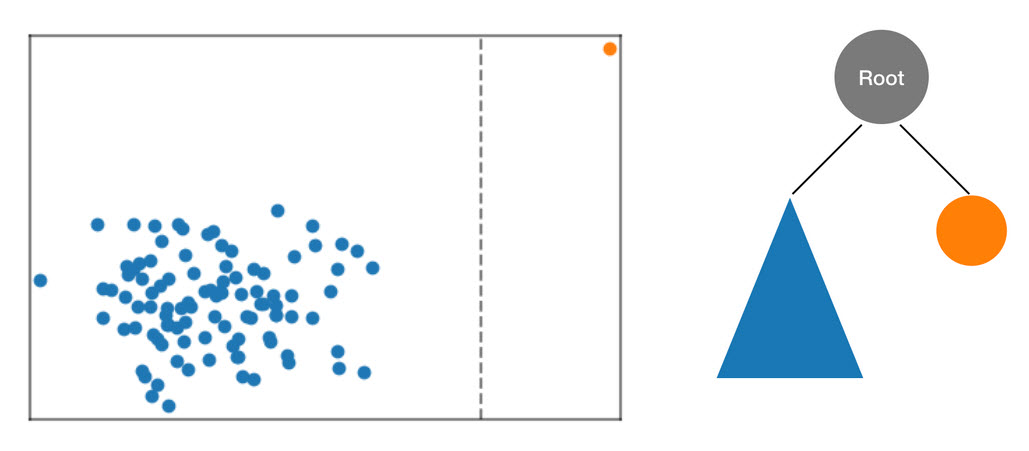
圖:除了一個異常資料點 (橘色) 之外,大多數資料位於叢集 (藍色) 中的二維資料集。樹狀結構會從根節點起始。
RCF 演算法會先計算資料的邊界方塊、選取隨機維度 (將更多權重調整為具有較高「變異」的維度),然後隨機判斷超平面「切割」在該維度中的位置,藉此在樹狀結構中組織這些資料。雖產生的兩個子空間,會定義自己的子樹狀結構。在這個範例中,切割的動作正好將一個孤立點與其他的樣本分隔。所產生二元樹的第一層包含了兩個節點,其中一個節點將包含初步分割區左側資料點的子樹狀結構,另一個節點則代表右方的單一點。
圖形:隨機分割二維資料集。相較於其他資料點,異常的資料點在樹狀結構深度較小時,更有可能獨立隔離於具邊框的方塊中。
接著會計算含邊框方塊左半邊和右半邊的資料,這項程序會不斷重複進行,直到樹狀結構的所有葉節點都代表樣本的單一資料點。請注意,如果孤立點的距離夠遠,則隨機分割法更有可能產生隔離點。此項觀察的直覺印象,就是大致上來說,樹狀結構的深度與異常分數成反比。
使用訓練過的RCF模型執行推論時,最終異常分數會報告為每個樹狀目錄所報告分數之間的平均值。請注意,新的資料點通常不存在於樹狀結構中。若要決定與新資料點對應的分數,可將資料點插入到指定的樹狀結構中,接著會用等同於上述訓練程序的方式,來將該樹狀結構有效率地 (和暫時性地) 重組。也就是說,所產生的樹狀結構,就如同輸入的資料點是其中一個樣本,一開始就用來建構樹狀結構。所呈報的分數,會與樹狀結構內輸入點的深度呈反比。
選擇超參數
用於調整RCF模型的主要超參數為 num_trees和 num_samples_per_tree。增加 num_trees 會減少異常分數中所觀察到的雜訊,因為最終的分數是每個樹狀結構所呈報分數的平均值。雖然最理想的值會隨應用程式而有不同,我們建議您從使用 100 個樹狀結構開始,在分數雜訊與模型複雜度之間取得平衡。請注意,推論時間和樹狀結構的數量呈正比。雖然訓練時間也會有影響,不過這主要是由上述的蓄水池取樣演算法決定。
參數 num_samples_per_tree 與資料集中預期的異常項目密度有關。尤其應選擇 num_samples_per_tree,以讓 1/num_samples_per_tree 接近於異常資料對正常資料的比率。例如,如果在每個樹狀結構中使用了 256 個樣本,則我們會預期資料包含 1/256 的異常項目,或是約 0.4% 的時間。同樣地,此一超參數最理想的值會隨應用程式而有不同。
參考
-
Sudipto Guha、Nina Mishra、Gourav Roy 與 Okke Schrijvers。“採用強大隨機分割森林演算法的串流異常偵測機制。” 於 International Conference on Machine Learning,第 2712 至 2721 頁。2016 年。
-
Byung-Hoon Park、George Ostrouchov、Nagiza F. Samatova 與 Al Geist。“蓄水池式的隨機取樣法,以放回的方式從資料串流抽樣。” 在 2004 年國際資料探SIAM勘會議的繼續進行中,第 492-496 頁。工業與應用數學學會,2004。