Las traducciones son generadas a través de traducción automática. En caso de conflicto entre la traducción y la version original de inglés, prevalecerá la version en inglés.
El análisis de componentes principales (PCA) es un algoritmo de aprendizaje que reduce la dimensionalidad (número de características) dentro de un conjunto de datos mientras retiene toda la información posible.
PCA reduce la dimensionalidad mediante la búsqueda de un nuevo conjunto de características denominado componentes, que son los compuestos de las características originales que no son correlativas entre sí. El primer componente implica la máxima variabilidad posible en los datos y el segundo componente la segunda variabilidad máxima y así sucesivamente.
Se trata de un algoritmo de reducción de la dimensionalidad no supervisado. En el aprendizaje no supervisado, no se utilizan las etiquetas que pueden asociarse a los objetos en el conjunto de datos de capacitación.
Dada la entrada de una matriz con filas
en cada dimensión 1 * d, los datos se particionan en minilotes de filas y se distribuyen entre los nodos de capacitación (procesos de trabajo). Cada proceso de trabajo realiza entonces la computación de un resumen de sus datos. Los resúmenes de estos distintos procesos de trabajo se unifican en una solución única al final de la computación.
Modos
El algoritmo PCA de Amazon SageMaker AI utiliza uno de los dos modos para calcular estos resúmenes, según la situación:
-
normal: para conjuntos de datos con datos dispersos y un número moderado de observaciones y características.
-
aleatorio: para conjuntos de datos con un gran número de observaciones y características. Este modo utiliza un algoritmo de aproximación.
Como último paso del algoritmo, realiza la descomposición de valor singular en la solución unificada, a partir de la que se derivan los componentes principales.
Modo 1: Regular
Los procesos de trabajo computan de forma conjunta
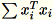y
.
nota
Como
son vectores de filas 1 * d,
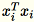es una matriz (no escalar). El uso de vectores de filas dentro del código nos permite obtener un almacenamiento en caché eficiente.
La matriz de covarianza se calcula como
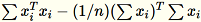y sus vectores singulares num_components superiores forman el modelo.
nota
Si subtract_mean es False, evitamos la computación y sustracción
.
Utilice este algoritmo cuando la dimensión d de los vectores sea lo suficientemente pequeña como para que
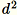pueda caber en la memoria.
Modo 2: Aleatorio
Cuando el número de características en el conjunto de datos de entrada es grande, utilizamos un método para aproximar la métrica de covarianza. Para cada minilote
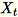de dimensión b * d, inicializamos de forma aleatoria una matriz (num_components + extra_components) * b que multiplicamos por cada minilote para crear una matriz (num_components + extra_components) * d. Los procesos de trabajo computan la suma de estas matrices y los servidores realizan el SVD en la matriz (num_components + extra_components) * d final. Los vectores singulares num_components de la parte superior derecha de ella son la aproximación de los vectores singulares superiores de la matriz de entrada.
Deje
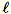
= num_components + extra_components. Con un minilote
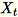de dimensión b * d, el proceso de trabajo dibuja una matriz aleatoria
de dimensión
. Según si el entorno utiliza una GPU o CPU y el tamaño de dimensión, la matriz es una matriz de firma aleatoria en la que cada entrada es +-1 o una FJLT (transformación rápida Johnson Lindenstrauss; para obtener más información, consulte Transformaciones FJLT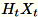
y mantiene
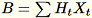. El proceso de trabajo también mantiene
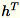, la suma de columnas de
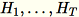(T que es el número total de minilotes) y s, la suma de todas las filas de entrada. Después de procesar el fragmento completo de datos, el proceso de trabajo envía el servidor B, h, s y n (el número de filas de entrada).
Indicar las entradas distintas en el servidor como
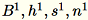El servidor computa B, h, s, n las sumas de las entradas respectivas. A continuación, computa
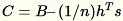y encuentra su descomposición de valores singular. Los vectores singulares de la parte superior derecha y los valores singulares de C se utilizan como la solución aproximada para el problema.
