Las traducciones son generadas a través de traducción automática. En caso de conflicto entre la traducción y la version original de inglés, prevalecerá la version en inglés.
Amazon SageMaker AI Random Cut Forest (RCF) es un algoritmo no supervisado para detectar puntos de datos anómalos en un conjunto de datos. Son observaciones que difieren de los datos bien estructurados y con patrones. Se pueden mostrar anomalías como picos inesperados en los datos de serie temporal, cortes en la periodicidad o puntos de datos inclasificables. Son fáciles de detectar. Cuando se visualizan en un gráfico, se suelen distinguir fácilmente de los datos "normales". La inclusión de estas anomalías en un conjunto de datos puede aumentar notablemente la complejidad de una tarea de machine learning, ya que los datos "normales" pueden describirse con frecuencia con un modelo sencillo.
La principal idea detrás del algoritmo RCF es crear un bosque de árboles donde cada árbol se obtenga mediante una partición de una muestra de los datos de capacitación. Por ejemplo, se determina por primera vez una muestra aleatoria de los datos de entrada. La muestra aleatoria se particiona después de acuerdo con el número de árboles del bosque. Se le proporciona a cada árbol una partición y se organiza ese subconjunto de puntos en un árbol k-d. La puntuación de anomalías que al árbol asigna a un punto de datos se define como el cambio previsto en la complejidad del árbol como resultado de la adición de ese punto al árbol que, aproximadamente, es inversamente proporcional a la profundidad resultante del punto en el árbol. El bosque de corte aleatorio asigna una puntuación de anomalías calculando la puntuación media de cada árbol constituyente y escalando el resultado en relación con el tamaño de la muestra. El algoritmo RCF se basa en el descrito en la referencia [1].
Datos de muestra de forma aleatoria
El primer paso del algoritmo RCF es obtener una muestra aleatoria de los datos de capacitación. En concreto, supongamos que deseamos una muestra de tamaño
 total
total
 de puntos de datos. Si los datos de capacitación son lo suficientemente pequeños, puede utilizarse el conjunto de datos completo y podríamos dibujar aleatoriamente
de puntos de datos. Si los datos de capacitación son lo suficientemente pequeños, puede utilizarse el conjunto de datos completo y podríamos dibujar aleatoriamente
 elementos a partir de este conjunto. Sin embargo, los datos de capacitación son normalmente demasiado grandes para ajustarlos todos a la vez y este enfoque no es factible. En su lugar, usamos una técnica llamada "muestreo de depósito".
elementos a partir de este conjunto. Sin embargo, los datos de capacitación son normalmente demasiado grandes para ajustarlos todos a la vez y este enfoque no es factible. En su lugar, usamos una técnica llamada "muestreo de depósito".
El muestreo de depósito en el que los elementos del conjunto de datos solo pueden observarse de uno en uno o en lotes. De hecho, el muestreo de depósito funciona incluso cuando
en el que los elementos del conjunto de datos solo pueden observarse de uno en uno o en lotes. De hecho, el muestreo de depósito funciona incluso cuando
 no se conoce a priori. Si solo se solicita una muestra, como cuando
no se conoce a priori. Si solo se solicita una muestra, como cuando
 , el algoritmo tiene el siguiente aspecto:
, el algoritmo tiene el siguiente aspecto:
Algoritmo: Muestreo de depósito
-
Entrada: conjunto de datos o transmisión de datos
 .
. -
Inicialice la muestra aleatoria
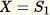 .
. -
Para cada muestra observada
 :
:-
Elija un número aleatorio uniforme
![Equation in text-form: \xi \in [0,1]](images/rcf6.jpg)
-
Si

-
Establezca

-
-
-
Devolución

Este algoritmo selecciona una muestra aleatoria de manera que
 para todos los
para todos los
 . Cuando
. Cuando
 , el algoritmo es más complicado. Además, debe realizarse una distinción entre el muestreo aleatorio con y sin reemplazo. RCF realiza un muestreo de depósito aumentado sin reemplazo en los datos de capacitación basado en los algoritmos descritos en [2].
, el algoritmo es más complicado. Además, debe realizarse una distinción entre el muestreo aleatorio con y sin reemplazo. RCF realiza un muestreo de depósito aumentado sin reemplazo en los datos de capacitación basado en los algoritmos descritos en [2].
Capacitar un modelo RFC y producir inferencias
El siguiente paso de RCF es construir un bosque de corte aleatorio con la muestra aleatoria de datos. En primer lugar, la muestra se particiona en el mismo número de particiones del mismo tamaño que el número de árboles del bosque. A continuación, se envía cada partición a un árbol individual. El árbol organiza de forma recursiva su partición en un árbol binario mediante la partición del dominio de datos en contornos delimitadores.
Este procedimiento puede entenderse mejor con un ejemplo. Supongamos que se proporciona a un árbol el siguiente conjunto de datos de dos dimensiones. El árbol correspondiente se inicializa en el nodo raíz:
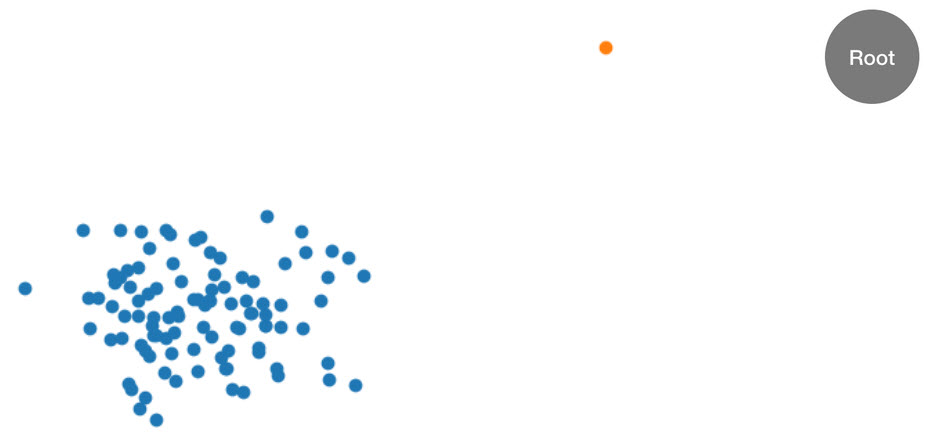
Figura: un conjunto de datos de bidimensional en el que la mayoría de los datos se encuentra en un clúster (azul), excepto en un punto de datos anómalo (naranja). El árbol se inicializa con un nodo raíz.
El algoritmo RCF organiza estos datos en un árbol procesando primero un contorno delimitador de los datos, seleccionando una dimensión aleatoria (proporcionando más peso a las dimensiones con una "varianza" superior) y, a continuación, determinando aleatoriamente la posición de un "corte" hiperplano en esa dimensión. Los dos subespacios resultantes definen su propio subárbol. En este ejemplo, se produce el corte para separar un punto aislado del resto de la muestra. El primer nivel del árbol binario resultante consta de dos nodos, uno de los cuales consistirá en el subárbol de puntos a la izquierda del corte inicial y el otro representará el punto único a la derecha.
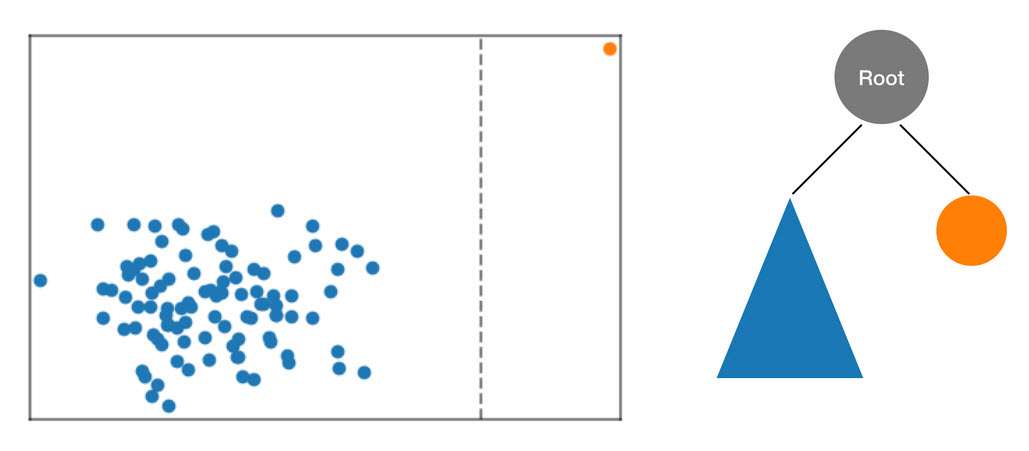
Figura: un corte aleatorio que realiza una partición del conjunto de datos bidimensional. Es más probable que un punto de datos anómalo quede aislado en un cuadro delimitador con una profundidad de árbol inferior que otros puntos.
Los cuadros delimitadores se procesan a continuación para las mitades izquierda y derecha de los datos, y se repite el proceso hasta que cada mitad del árbol represente un punto de datos único de la muestra. Tenga en cuenta que si el punto aislado está lo suficientemente alejado, es más probable que un corte aleatorio genere el aislamiento del punto. Esta observación es la razón por la que, en términos generales, la profundidad del árbol es inversamente proporcional a la puntuación de anomalías.
Al realizar una inferencia mediante un modelo de RCF capacitado, la puntuación de anomalías final se expresa como la media de las puntuaciones notificadas por cada árbol. Tenga en cuenta que normalmente el nuevo punto de datos no se encuentra aún en el árbol. Para determinar la puntuación asociada al nuevo punto de datos, el punto de dato se inserta en el árbol determinado y este se vuelve a ensamblar de forma eficiente (y temporal) de manera equivalente al proceso de capacitación descrito anteriormente. Es decir, el árbol resultante es como si el punto de datos de entrada fuese un miembro de la muestra utilizada para crear el árbol en el primer lugar. La puntuación notificada es inversamente proporcional a la profundidad del punto de entrada en el árbol.
Elegir hiperparámetros
Los hiperparámetros principales utilizados para ajustar el modelo RCF son num_trees y num_samples_per_tree. El aumento de num_trees tiene el efecto de reducción del ruido observado en las puntuaciones de anomalías, puesto que la puntuación final es la media de puntuaciones notificadas por cada árbol. Aunque el valor óptimo depende de la aplicación, le recomendamos que utilice 100 árboles para comenzar con un equilibrio entre la complejidad del modelo y el ruido de la puntuación. Tenga en cuenta que el tiempo de inferencia es proporcional a los números de árboles. Aunque tiempo de capacitación también se ve afectado, se encuentra dominado por el algoritmo de muestreo de depósito descrito anteriormente.
El parámetro num_samples_per_tree está relacionado con la densidad prevista de anomalías en el conjunto de datos. En particular, debe elegirse num_samples_per_tree de forma que 1/num_samples_per_tree se aproxime a la proporción de datos anómalos en los datos normales. Por ejemplo, si se utilizan 256 muestras en cada árbol, esperamos que nuestros datos contengan 1 de 256 anomalías u ocupen aproximadamente el 0,4% del tiempo. Una vez más, un valor óptimo para este hiperparámetro depende de la aplicación.
Referencias
-
Sudipto Guha, Nina Mishra, Gourav Roy y Okke Schrijvers. "Robust random cut forest based anomaly detection on streams". En International Conference on Machine Learning, pg. 2712-2721. 2016.
-
Byung-Hoon Park, George Ostrouchov, Nagiza F. Samatova y Al Geist. "Reservoir-based random sampling with replacement from data stream". En Proceedings of the 2004 SIAM International Conference on Data Mining, pp. 492-496. Society for Industrial and Applied Mathematics, 2004.