Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.
Amazon SageMaker AI Random Cut Forest (RCF) ist ein unbeaufsichtigter Algorithmus zur Erkennung anomaler Datenpunkte innerhalb eines Datensatzes. Das sind Beobachtungen, die von ansonsten gut strukturierten oder nach Mustern geordneten Daten abweichen. Solche Auffälligkeiten können sich als unerwartete Spitzen in Zeitreihendaten, unterbrochener Periodizität oder unklassifizierbaren Datenpunkten manifestieren. Sie sind einfach zu beschreiben, denn wenn sie in einem Diagramm dargestellt werden, sind sie meist leicht von "regulären" Daten unterscheidbar. Sind diese Anomalien in einem Datensatz enthalten, kann dies zu einer erheblichen Komplexitätssteigerung einer Machine-Learning-Aufgabe führen, da sich "reguläre" Daten häufig in einem einfachen Modell darstellen lassen.
Das Grundkonzept hinter dem Algorithmus von RCF besteht darin, eine Gesamtstruktur (Forest) zu erstellen, in der jede einzelne Struktur (Baum) mithilfe einer Partition aus der Trainingsdaten-Stichprobe abgerufen wird. Beispielsweise wird zunächst eine zufällige Stichprobe aus den Eingabedaten gezogen. Diese randomisierte Stichprobe wird dann entsprechend der Anzahl der Einzelstrukturen in der Gesamtstruktur partitioniert. Jede Struktur erhält eine solche Partition und organisiert ein Punkte-Subset in einer k-d-Struktur. Die Anomaliebewertung, die einem Datenpunkt von einer Struktur zugeordnet wurde, wird als erwartete Änderung der Strukturkomplexität definiert, wenn der Struktur dieser Punkt hinzugefügt wird. Dies verhält sich umgekehrt proportional zur resultierenden Tiefe des Punkts in der Struktur. Random Cut Forest weist die Anomaliebewertung durch Berechnung der durchschnittlichen Bewertung jeder einzelnen Struktur und Skalierung des Ergebnisses unter Berücksichtigung der Stichprobengröße zu. Der RCF-Algorithmus basiert auf dem in Referenz [1] beschriebenen Algorithmus.
Datenstichprobe nach dem Zufallsprinzip
Der erste Schritt im RCF-Algorithmus besteht darin, eine zufällige Stichprobe der Trainingsdaten zu entnehmen. Angenommen, wir möchten ein Beispiel der Größe
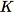 von
von
 Datenpunkten insgesamt sampeln. Sind das Trainingsdaten klein genug, kann der gesamte Datensatz verwendet werden und es könnten
Datenpunkten insgesamt sampeln. Sind das Trainingsdaten klein genug, kann der gesamte Datensatz verwendet werden und es könnten
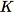 Elemente nach dem Zufallsprinzip aus diesem Datensatz gezogen werden. Meist sind das Trainingsdaten jedoch zu umfangreich, um alle einzubeziehen, daher ist dieses Verfahren nicht anwendbar. Stattdessen wird eine als "Reservoir-Sampling" bezeichnete Methode genutzt.
Elemente nach dem Zufallsprinzip aus diesem Datensatz gezogen werden. Meist sind das Trainingsdaten jedoch zu umfangreich, um alle einzubeziehen, daher ist dieses Verfahren nicht anwendbar. Stattdessen wird eine als "Reservoir-Sampling" bezeichnete Methode genutzt.
Reservoir-Sampling , wobei die Elemente im Datensatz nur einzeln oder in Stapeln beobachtet werden können. Tatsächlich funktioniert Reservoir-Sampling auch dann, wenn
, wobei die Elemente im Datensatz nur einzeln oder in Stapeln beobachtet werden können. Tatsächlich funktioniert Reservoir-Sampling auch dann, wenn
 nicht a priori bekannt ist. Wenn nur eine Stichprobe angefordert wird, z. B. wenn
nicht a priori bekannt ist. Wenn nur eine Stichprobe angefordert wird, z. B. wenn
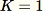 , sieht der Algorithmus wie folgt aus:
, sieht der Algorithmus wie folgt aus:
Algorithmus: Reservoir-Sampling
-
Eingabe: Datensatz oder Datenstrom

-
Initialisieren der zufälligen Stichprobe
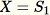
-
Für jede beobachtete Stichprobe
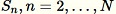 :
:-
Auswählen einer einheitlichen Zufallszahl
![Equation in text-form: \xi \in [0,1]](images/rcf6.jpg)
-
Wenn

-
Legen Sie
 fest.
fest.
-
-
-
Ergebnis

Dieser Algorithmus wählt eine zufällige Stichprobe mit
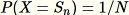 für alle
für alle
 aus. Wenn
aus. Wenn
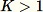 zutrifft, ist der Algorithmus komplizierter. Außerdem muss zwischen zufälligen Stichproben mit und ohne Ersetzung unterschieden werden. RCF führt ein erweitertes Reservoir-Sampling ohne Ersetzung mit den Trainingsdaten auf Basis der in [2] beschriebenen Algorithmen aus.
zutrifft, ist der Algorithmus komplizierter. Außerdem muss zwischen zufälligen Stichproben mit und ohne Ersetzung unterschieden werden. RCF führt ein erweitertes Reservoir-Sampling ohne Ersetzung mit den Trainingsdaten auf Basis der in [2] beschriebenen Algorithmen aus.
Schulen eines RFC-Modells und Erstellen von Inferenzen
Der nächste RCF-Schritt ist eine Random Cut Forest-Erstellung mithilfe der zufälligen Datenstichprobe. Zunächst wird die Stichprobe in gleich große Partitionen partitioniert. Die Anzahl der Partitionen entspricht der Anzahl der Strukturen in der Gesamtstruktur. Anschließend wird jede Partition an eine einzelne Struktur gesendet. Die Struktur organisiert die eigene Partition rekursiv in eine binäre Struktur, indem sie die Datendomain in Begrenzungsrahmen partitioniert.
Dieses Verfahren lässt sich am besten anhand eines Beispiels darstellen. Angenommen, eine Struktur erhält folgenden zweidimensionalen Datensatz. Die entsprechende Struktur wird mit dem Stammknoten initialisiert:

Abbildung: Ein zweidimensionaler Datensatz, bei dem die meisten Daten in einem Cluster (blau) liegen, mit Ausnahme eines anomalen Datenpunkts (orange). Die Struktur wird mit einem Stammknoten initialisiert.
Der RCF-Algorithmus organisiert diese Daten in einer Struktur. Dazu wird zunächst ein Begrenzungsrahmen der Daten berechnet und eine Zufallsdimension ausgewählt (dabei haben Dimensionen mit höherer "Varianz" Vorrang). Anschließend wird die Position eines "Schnitts" durch die Hyperebene der Dimension per Zufallsprinzip ermittelt. Die daraus entstehenden Teilräume definieren ihre eigene Unterstruktur. In diesem Beispiel wird durch den Schnitt ein einzelner Punkt vom Rest der Stichprobe getrennt. Die erste Ebene der resultierenden Binärstruktur umfasst zwei Knoten. Einer enthält die Unterstruktur der Punkte links vom erfolgten Schnitt, der andere stellt den einzelnen Punkt auf der rechten Seite dar.
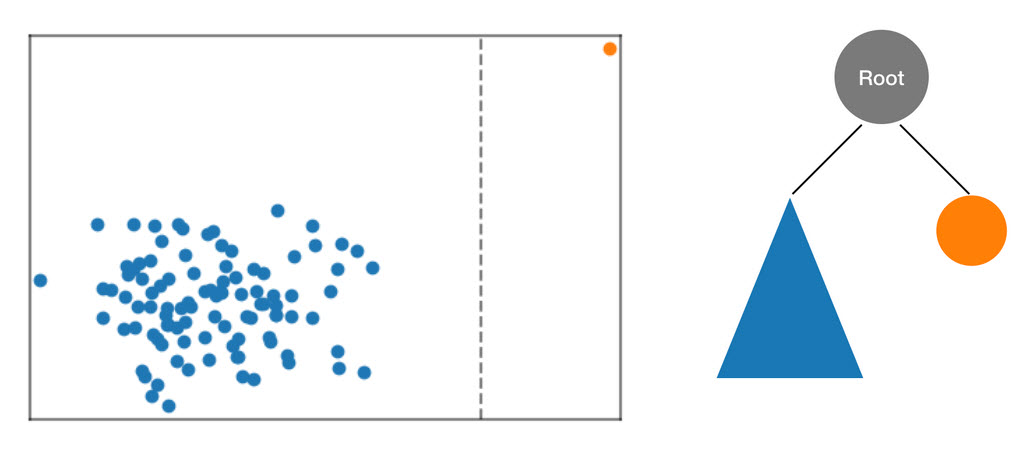
Abbildung: Ein zufälliger Schnitt, der den zweidimensionalen Datensatz partitioniert. Bei einem anormalen Datenpunkt ist die Wahrscheinlichkeit, dass dieser isoliert in einem Begrenzungsrahmen in geringerer Strukturtiefe liegt, höher als bei anderen Punkten.
Danach werden Begrenzungsrahmen für die linke und die rechte Hälfte der Daten berechnet. Dieser Prozess wird so lange wiederholt, bis alle Endknoten der Struktur einen einzelnen Datenpunkt aus der Stichprobe darstellen. Wenn der einzelne Punkt weit genug weg liegt, ist die Wahrscheinlichkeit, dass ein zufälliger Schnitt zur Isolierung des Punkts führt, höher. Diese Beobachtung führt zur Annahme, dass die Strukturtiefe praktisch umgekehrt proportional zur Anomaliebewertung ist.
Bei der Inferenzausführung mithilfe eines trainierten RCF-Modells wird die finale Anomaliebewertung aus dem Mittelwert der von jeder einzelnen Struktur gemeldeten Bewertung berechnet. Beachten Sie, dass der neue Datenpunkt in der Struktur häufig noch nicht vorhanden ist. Um die Bewertung für den neuen Datenpunkt zu ermitteln, wird der Datenpunkt in die vorhandene Struktur eingefügt. Diese Struktur wird dann effizient (und temporär) auf dieselbe Weise wie oben im Trainingsverfahren beschrieben neu aufgebaut. Das heißt, die resultierende Struktur sieht aus, als ob der Eingabedatenpunkt Teil der Stichprobe gewesen wäre, aus der die Struktur zuerst generiert wurde. Die gemeldete Bewertung verhält sich umgekehrt proportional zur Tiefe des Eingabepunkts in der Struktur.
Auswählen von Hyperparametern
Zur Optimierung des RCF-Modells werden in erster Linie die Hyperparameter num_trees und num_samples_per_tree verwendet. Eine Erhöhung von num_trees führt zu einer Reduzierung der Stördaten in Anomaliebewertungen, da die finale Bewertung aus dem Mittelwert der von den einzelnen Strukturen gemeldeten Bewertungen entsteht. Der optimale Wert ist abhängig von der Anwendung, aber wir empfehlen, zu Beginn 100 Strukturen zu verwenden, um ein Gleichgewicht zwischen Stördaten in der Bewertung und Modellkomplexität zu schaffen. Beachten Sie, dass sich die Inferenzzeit proportional zur Anzahl der Strukturen verhält. Obwohl auch die Trainingszeit betroffen ist, wird sie vom oben beschriebenen Reservoir-Sampling-Algorithmus dominiert.
Der Parameter num_samples_per_tree bezieht sich auf die erwartete Anomaliedichte im Datensatz. Insbesondere num_samples_per_tree sollte so gewählt werden, dass 1/num_samples_per_tree dem Verhältnis von anormalen Daten zu normalen Daten entspricht. Wenn beispielsweise 256 Stichproben pro Struktur verwendet werden, erwarten wir, dass die Daten Anomalien im Verhältnis von 1/256 oder ca. 0,4 % der Zeit aufweisen. Auch hier gilt, dass der optimale Wert für diesen Hyperparameter von der Anwendung abhängt.
Referenzen
-
Sudipto Guha, Nina Mishra, Gourav Roy und Okke Schrijvers. "Robust random cut forest based anomaly detection on streams." In International Conference on Machine Learning, pp. 2712-2721. 2016.
-
Byung-Hoon Park, George Ostrouchov, Nagiza F. Samatova und Al Geist. "Reservoir-based random sampling with replacement from data stream." In Proceedings of the 2004 SIAM International Conference on Data Mining, pp. 492-496. Society for Industrial and Applied Mathematics, 2004.