Le traduzioni sono generate tramite traduzione automatica. In caso di conflitto tra il contenuto di una traduzione e la versione originale in Inglese, quest'ultima prevarrà.

Comprensione dei sistemi di coordinate e della fusione dei sensori

I dati della nuvola di punti si trovano sempre in un sistema di coordinate. Questo sistema di coordinate può essere locale per il veicolo o il dispositivo che rileva l'ambiente circostante oppure può essere un sistema di coordinate mondiali. Quando si utilizzano processi di etichettatura con nuvole di punti Ground Truth 3D, tutte le annotazioni vengono generate utilizzando il sistema di coordinate dei dati di input. Per alcuni tipi di attività e funzionalità di etichettatura dei processi, è necessario fornire i dati in un sistema di coordinate mondiali

In questo argomento verranno illustrate le seguenti informazioni:

Coordinamento dei requisiti di sistema per i processi di etichettatura

Se i dati della nuvola di punti sono stati raccolti in un sistema di coordinate locale, è possibile utilizzare una matrice estrinseca del sensore utilizzato per raccogliere i dati per convertirli in un sistema di coordinate mondiali o in un quadro di riferimento globale. Se non è possibile ottenere una matrice estrinseca per i dati della nuvola di punti e, di conseguenza, non è possibile ottenere nuvole di punti in un sistema di coordinate mondiale, è possibile fornire dati di nuvole di punti in un sistema di coordinate locale per i tipi di attività di rilevamento di oggetti nuvola di punti 3D e segmentazione semantica.

Per il tracciamento degli oggetti, è necessario fornire i dati della nuvola di punti in un sistema di coordinate mondiale. Questo perché quando si tracciano oggetti su più frame, il veicolo ego stesso si muove nel mondo e quindi tutti i frame hanno bisogno di un punto di riferimento.

Se si includono i dati della fotocamera per la fusione dei sensori, si consiglia di fornire le pose della telecamera nello stesso sistema di coordinate mondiali del sensore 3D (ad esempio un DAR sensore Li).

Utilizzo dei dati delle nuvole di punti in un sistema di coordinate mondiali

Questa sezione spiega cos'è un sistema di coordinate mondiale (WCS), noto anche come sistema di riferimento globale, e spiega come è possibile fornire dati di nuvole di punti in un sistema di coordinate globali.

Che cos'è un sistema di coordinate mondiali?

Un sistema di riferimento WCS o globale è un sistema di coordinate universale fisso in cui sono collocati i sistemi di coordinate di veicoli e sensori. Ad esempio, se più frame di nuvole di punti si trovano in sistemi di coordinate diversi perché sono stati raccolti da due sensori, è WCS possibile utilizzare a per tradurre tutte le coordinate di questi frame a nuvola di punti in un unico sistema di coordinate, in cui tutti i frame hanno la stessa origine, (0,0,0). Questa trasformazione viene eseguita traducendo l'origine di ogni fotogramma nell'origine di WCS utilizzando un vettore di traslazione e ruotando i tre assi (tipicamente x, y e z) con il giusto orientamento utilizzando una matrice di rotazione. Questa trasformazione del corpo rigido è chiamata trasformazione omogenea.

Un sistema di coordinate mondiali è importante per la pianificazione globale dei percorsi, la localizzazione, la mappatura e la gestione delle simulazioni degli scenari. Ground Truth utilizza il sistema di coordinate mondiali cartesiane destrorso come quello definito in ISO8855, in cui l'asse x è in avanti verso il movimento dell'auto, l'asse y è a sinistra e l'asse z punta verso l'alto da terra.

Il quadro globale di riferimento dipende dai dati. Alcuni set di dati utilizzano la DAR posizione Li nel primo frame come origine. In questo scenario, tutti i frame utilizzano il primo frame come riferimento e l'intestazione e la posizione del dispositivo saranno vicini all'origine nel primo frame. Ad esempio, KITTI i set di dati hanno il primo frame come riferimento per le coordinate mondiali. Altri set di dati forniscono una posizione del dispositivo che è diversa dall'origine.

Nota che questo non è il sistema di IMU coordinateGPS/, che in genere viene ruotato di 90 gradi lungo l'asse z. Se i dati della nuvola di punti si trovano in un sistema di IMU coordinateGPS/(come OxTS nel KITTI set di dati AV open source), è necessario trasformare l'origine in un sistema di coordinate mondiale (in genere il sistema di coordinate di riferimento del veicolo). È possibile applicare questa trasformazione moltiplicando i dati con i parametri di trasformazione (matrice di rotazione e vettore di traslazione). Questo trasformerà i dati dal suo sistema di coordinate originale in un sistema di coordinate di riferimento globale. Ulteriori informazioni su questa trasformazione sono disponibili nella sezione successiva.

Converti i dati di una nuvola di punti 3D in un WCS

Ground Truth presuppone che i dati della nuvola di punti siano già stati trasformati in un sistema di coordinate di riferimento scelto. Ad esempio, è possibile scegliere il sistema di coordinate di riferimento del sensore (ad esempio LiDAR) come sistema di coordinate di riferimento globale. È inoltre possibile prendere nuvole di punti da vari sensori e trasformarle dalla vista del sensore alla vista del sistema di coordinate di riferimento del veicolo. Utilizzate la matrice estrinseca del sensore, composta da una matrice di rotazione e un vettore di traslazione, per convertire i dati della nuvola di punti in un sistema di riferimento WCS o globale.

Collettivamente, il vettore di traslazione e la matrice di rotazione possono essere utilizzati per creare una matrice estrinseca, che può essere utilizzata per convertire i dati da un sistema di coordinate locale a. WCS Ad esempio, la matrice DAR estrinseca Li può essere composta come segue, dove si trova la matrice di rotazione e il R vettore di traslazione: T

LiDAR_extrinsic = [R T;0 0 0 1]

Ad esempio, il KITTI set di dati per la guida autonoma include una matrice di rotazione e un vettore di traslazione per la matrice di trasformazione DAR estrinseca Li per ogni frame. Il modulo pykitti python può essere usato per caricare i dati e nel set di KITTI dati dataset.oxts[i].T_w_imu fornisce la trasformazione DAR estrinseca Li per il frame i ^th che può essere moltiplicato con i punti in quel frame per convertirli in un frame mondiale -. np.matmul(lidar_transform_matrix, points) La moltiplicazione di un punto in un DAR frame Li con una matrice estrinseca Li lo trasforma in coordinate mondiali. DAR Moltiplicando un punto nel frame mondiale con la matrice estrinseca della telecamera, si ottengono le coordinate del punto nel frame di riferimento della telecamera.

Il seguente esempio di codice mostra come convertire i frame a nuvole di punti dal set di dati in un. KITTI WCS

import pykitti
import numpy as np

basedir = '/Users/nameofuser/kitti-data'
date = '2011_09_26'
drive = '0079'

# The 'frames' argument is optional - default: None, which loads the whole dataset.
# Calibration, timestamps, and IMU data are read automatically. 
# Camera and velodyne data are available via properties that create generators
# when accessed, or through getter methods that provide random access.
data = pykitti.raw(basedir, date, drive, frames=range(0, 50, 5))

# i is frame number
i = 0

# lidar extrinsic for the ith frame
lidar_extrinsic_matrix = data.oxts[i].T_w_imu

# velodyne raw point cloud in lidar scanners own coordinate system
points = data.get_velo(i)

# transform points from lidar to global frame using lidar_extrinsic_matrix
def generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix):
    tps = []
    for point in points:
        transformed_points = np.matmul(lidar_extrinsic_matrix, np.array([point[0], point[1], point[2], 1], dtype=np.float32).reshape(4,1)).tolist()
        if len(point) > 3 and point[3] is not None:
            tps.append([transformed_points[0][0], transformed_points[1][0], transformed_points[2][0], point[3]])
       
    return tps
    
# customer transforms points from lidar to global frame using lidar_extrinsic_matrix
transformed_pcl = generate_transformed_pcd_from_point_cloud(points, lidar_extrinsic_matrix)    

Fusione dei sensori

Ground Truth supporta la fusione dei sensori dei dati della nuvola di punti con un massimo di 8 ingressi di videocamere. Questa funzione consente agli etichettatori umani di visualizzare il fotogramma a nuvola di punti 3D side-by-side con il fotogramma video sincronizzato. Oltre a fornire un contesto visivo più ampio per l'etichettatura, la fusione dei sensori consente ai worker di regolare le annotazioni nella scena 3D e nelle immagini 2D e la regolazione viene proiettata nell'altra vista. Il video seguente mostra un lavoro di etichettatura 3D con nuvole di punti con Li DAR e la fusione di sensori della fotocamera.

Per ottenere i migliori risultati, quando si utilizza la fusione di sensori, la nuvola di punti dovrebbe trovarsi in un. WCS Ground Truth utilizza le informazioni sul sensore (come LiDAR), sulla fotocamera e sulla posa del veicolo ego per calcolare matrici estrinseche e intrinseche per la fusione dei sensori.

Matrice estrinseca

Ground Truth utilizza matrici estrinseche del sensore (come LiDAR) e matrici estrinseche e intrinseche della fotocamera per proiettare oggetti da e verso il quadro di riferimento dei dati della nuvola di punti al quadro di riferimento della telecamera.

Ad esempio, per proiettare un'etichetta dalla nuvola di punti 3D al piano dell'immagine della telecamera, Ground Truth trasforma i punti 3D dal sistema DAR di coordinate di Li al sistema di coordinate della fotocamera. Questo viene in genere fatto prima trasformando i punti 3D dal sistema di coordinate DAR di Li in un sistema di coordinate mondiale (o un sistema di riferimento globale) utilizzando la matrice DAR estrinseca Li. Ground Truth utilizza quindi l'estrinseco inverso della telecamera (che converte i punti da un quadro di riferimento globale al quadro di riferimento della telecamera) per trasformare i punti 3D del sistema di coordinate mondiali ottenuto nella fase precedente nel piano dell'immagine della telecamera. La matrice DAR estrinseca Li può essere utilizzata anche per trasformare i dati 3D in un sistema di coordinate mondiale. Se i dati 3D sono già trasformati in un sistema di coordinate mondiali, la prima trasformazione non ha alcun impatto sulla traslazione delle etichette e la traslazione delle etichette dipende solo dall'estrinseca inversa della telecamera. Una matrice di viste viene utilizzata per visualizzare le etichette proiettate. Per ulteriori informazioni su queste trasformazioni e sulla matrice della visualizzazione, consulta Trasformazioni della fusione dei sensori Ground Truth.

Ground Truth calcola queste matrici estrinseche utilizzando Li DAR e i dati di posa della fotocamera forniti dall'utente: heading (in quaternioni:qx,, e) e (, qyqz,). qw position x y z Per il veicolo, tipicamente la direzione e la posizione sono descritte nel quadro di riferimento del veicolo in un sistema di coordinate mondiali e sono chiamate posa di un veicolo ego. Per ogni telecamera estrinseca, è possibile aggiungere informazioni sulla posa per quella telecamera. Per ulteriori informazioni, consulta Posa.

Matrice intrinseca

Ground Truth utilizza le matrici estrinseche e intrinseche della telecamera per calcolare i parametri di visualizzazione per trasformare le etichette da e verso la scena 3D alle immagini della telecamera. Ground Truth calcola la matrice intrinseca della telecamera utilizzando la lunghezza focale della stessa (fx, fy) e le coordinate del centro ottico (cx, cy) fornite dall'utente. Per ulteriori informazioni, consulta Intrinseca e distorsione.

Distorsione immagine

La distorsione dell'immagine può verificarsi per una serie di motivi. Ad esempio, le immagini possono essere distorte a causa degli effetti barile o fish-eye. Ground Truth utilizza parametri intrinsechi insieme al coefficiente di distorsione per non distorcere le immagini fornite durante la creazione di processi di etichettatura con nuvole di punti 3D. Se la distorsione di un'immagine della telecamera è già stata annullata, tutti i coefficienti di distorsione devono essere impostati su 0.

Per ulteriori informazioni sulle trasformazioni eseguite da Ground Truth per annullare la distorsione delle immagini, consulta Calibrazioni telecamera: estrinseca, intrinseca e distorsione.

Veicolo Ego

Per raccogliere dati per applicazioni di guida autonome, le misurazioni utilizzate per generare dati di nuvole di punti vengono prese da sensori montati su un veicolo o sul veicolo ego. Per proiettare le regolazioni delle etichette da e verso la scena 3D e le immagini 2D, Ground Truth richiede che il veicolo ego si trovi in un sistema di coordinate mondiali. La posizione del veicolo ego comprende coordinate di posizione e quaternione di orientamento.

Ground Truth usa la posa del veicolo ego per calcolare le matrici di rotazione e le trasformazioni. Le rotazioni in 3 dimensioni possono essere rappresentate da una sequenza di 3 rotazioni intorno a una sequenza di assi. In teoria, tre assi che attraversano lo spazio euclideo 3D sono sufficienti. In pratica, gli assi di rotazione sono scelti come vettori di base. Si prevede che le tre rotazioni rientrino in un sistema di riferimento globale (estrinseco). Ground Truth non ha un sistema di riferimento (intrinseco) centrato sul corpo di supporto che è collegato all’oggetto in rotazione e si muove con esso. Per tracciare gli oggetti, Ground Truth deve misurare da un riferimento globale in cui tutti i veicoli sono in movimento. Quando si utilizzano processi di etichettatura di nuvole di punti Ground Truth 3D, z specifica l'asse di rotazione (rotazione estrinseca) e gli angoli di Eulero di imbardata sono espressi in radianti (angolo di rotazione).

Posa

Ground Truth utilizza le informazioni di posa per le visualizzazioni 3D e la fusione dei sensori. Le informazioni di posa inserite attraverso il file manifest vengono utilizzate per calcolare matrici estrinseche. Se si dispone già di una matrice estrinseca, è possibile utilizzarla per estrarre i dati del sensore e della posa della telecamera.

Ad esempio, nel KITTI set di dati per la guida autonoma, il modulo pykitti python può essere utilizzato per caricare i dati. KITTI Nel set di dati dataset.oxts[i].T_w_imu fornisce la trasformata DAR estrinseca Li per il frame i ^th e può essere moltiplicata per i punti per inserirli in una cornice mondiale -. matmul(lidar_transform_matrix, points) Questa trasformazione può essere convertita in posizione (vettore di traduzione) e intestazione (in quaternione) di Li per il formato del file manifest di input. DAR JSON La trasformazione estrinseca della telecamera per cam0 nel i^° frame può essere calcolata da inv(matmul(dataset.calib.T_cam0_velo, inv(dataset.oxts[i].T_w_imu))) e questo può essere convertito in titolo e posizione per cam0.

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin= [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R

# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))

# heading in WCS using scipy 
heading = r.as_quat()
print(f"pose:{position}\nheading: {heading}")

Posizione

Nel file manifest di input, position si riferisce alla posizione del sensore rispetto a un frame mondiale. Se non riesci a inserire la posizione del dispositivo in un sistema di coordinate globali, puoi utilizzare DAR i dati Li con coordinate locali. Allo stesso modo, per le videocamere montate è possibile specificare la posizione e l'intestazione in un sistema di coordinate mondiali. Per la telecamera, se non si dispone di informazioni sulla posizione, utilizzare (0, 0, 0).

Di seguito sono riportati i campi nell'oggetto posizione:

Di seguito è riportato un esempio di position JSON oggetto:

{
    "position": {
        "y": -152.77584902657554,
        "x": 311.21505956090624,
        "z": -10.854137529636024
      }
}

Heading

Nel file manifest di input, heading è un oggetto che rappresenta l'orientamento di un dispositivo rispetto al frame mondiale. I valori delle intestazioni devono essere in quaternione. Un quaternione è una rappresentazione dell'orientamento coerente con le proprietà sferiche geodesiche. Se non riesci a inserire l'intestazione del sensore nelle coordinate mondiali, usa il quaternione dell'identità (qx = 0, qy = 0, qz = 0, qw = 1). Allo stesso modo, per le telecamere, specifica l'intestazione in quaternioni. Se non riesci a ottenere parametri estrinseci di calibrazione della telecamera, utilizza anche il quaternione di identità.

I campi nell'oggetto heading sono i seguenti:

Quello che segue è un esempio di heading JSON oggetto:

{
    "heading": {
        "qy": -0.7046155108831117,
        "qx": 0.034278837280808494,
        "qz": 0.7070617895701465,
        "qw": -0.04904659893885366
      }
}

Per ulteriori informazioni, consulta Calcolo dei quaternioni e della posizione di orientamento.

Calcolo dei quaternioni e della posizione di orientamento

Ground Truth richiede che tutti i dati di orientamento, o intestazione, siano forniti in quaternioni. Un quaternione è una rappresentazione dell'orientamento coerente con proprietà sferiche geodesiche che possono essere utilizzate per approssimare la rotazione. Rispetto agli angoli di Eulero sono più semplici da comporre ed evitano il problema del blocco cardanico. Rispetto alle matrici di rotazione sono più compatti, più stabili numericamente e più efficienti.

È possibile calcolare quaternioni da una matrice di rotazione o da una matrice di trasformazione.

Se si dispone di una matrice di rotazione (composta dalle rotazioni degli assi) e vettore di traslazione (o origine) nel sistema di coordinate mondiali invece di una singola matrice di trasformazione rigida 4x4, è possibile utilizzare direttamente la matrice di rotazione e il vettore di traslazione per calcolare i quaternioni. Librerie come scipy e pyqaternion possono aiutare. Il seguente blocco di codice mostra un esempio che utilizza queste librerie per calcolare il quaternione da una matrice di rotazione.

import numpy

rotation = [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03],
 [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02],
 [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01]]
 
origin = [1.71104606e+00,
          5.80000039e-01,
          9.43144935e-01]

         
from scipy.spatial.transform import Rotation as R
# position is the origin
position = origin 
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Anche uno strumento UI come il 3D Rotation Converter può essere utile.

Se si dispone di una matrice di trasformazione estrinseca 4x4, si noti che la matrice di trasformazione è nel formato [R T; 0 0 0 1] dove R è la matrice di rotazione e T è il vettore di traslazione dell'origine. Ciò significa che è possibile estrarre la matrice di rotazione e il vettore di traslazione dalla matrice di trasformazione come segue.

import numpy as np

transformation 
= [[ 9.96714314e-01, -8.09890350e-02,  1.16333982e-03, 1.71104606e+00],
   [ 8.09967396e-02,  9.96661051e-01, -1.03090934e-02, 5.80000039e-01],
   [-3.24531964e-04,  1.03694477e-02,  9.99946183e-01, 9.43144935e-01],
   [              0,               0,               0,              1]]

transformation  = np.array(transformation )
rotation = transformation[0:3][0:3]
translation= transformation[0:3][3]

from scipy.spatial.transform import Rotation as R
# position is the origin translation
position = translation
r = R.from_matrix(np.asarray(rotation))
# heading in WCS using scipy 
heading = r.as_quat()
print(f"position:{position}\nheading: {heading}")

Con la propria configurazione, è possibile calcolare una matrice di trasformazione estrinseca utilizzando la IMU posizione e l'orientamentoGPS/(latitudine, longitudine, altitudine e rollio, inclinazione, imbardata) rispetto al sensore Li sul veicolo ego. DAR Ad esempio, è possibile calcolare la posa da dati KITTI grezzi utilizzando per trasformare i dati oxts in pose pose = convertOxtsToPose(oxts) euclidee locali, specificate da matrici di trasformazione rigide 4x4. Puoi quindi trasformare questa matrice di trasformazione posa in un frame di riferimento globale utilizzando la matrice di trasformazione dei frame di riferimento nel sistema di coordinate mondiali.

struct Quaternion
{
    double w, x, y, z;
};

Quaternion ToQuaternion(double yaw, double pitch, double roll) // yaw (Z), pitch (Y), roll (X)
{
    // Abbreviations for the various angular functions
    double cy = cos(yaw * 0.5);
    double sy = sin(yaw * 0.5);
    double cp = cos(pitch * 0.5);
    double sp = sin(pitch * 0.5);
    double cr = cos(roll * 0.5);
    double sr = sin(roll * 0.5);

    Quaternion q;
    q.w = cr * cp * cy + sr * sp * sy;
    q.x = sr * cp * cy - cr * sp * sy;
    q.y = cr * sp * cy + sr * cp * sy;
    q.z = cr * cp * sy - sr * sp * cy;

    return q;
}

Trasformazioni della fusione dei sensori Ground Truth

Le sezioni seguenti illustrano in modo più dettagliato le trasformazioni di fusione dei sensori Ground Truth eseguite utilizzando i dati di posa forniti.

Li Extrinsic DAR

Per proiettare da e verso una DAR scena 3D Li su un'immagine di una telecamera 2D, Ground Truth calcola le rigide metriche di proiezione della trasformazione utilizzando la posa e la direzione del veicolo ego. Ground Truth calcola la rotazione e la traslazione delle coordinate di un mondo nel piano 3D eseguendo una semplice sequenza di rotazioni e traslazioni.

Ground Truth calcola i parametri di rotazione utilizzando i quaternioni di intestazione come segue:

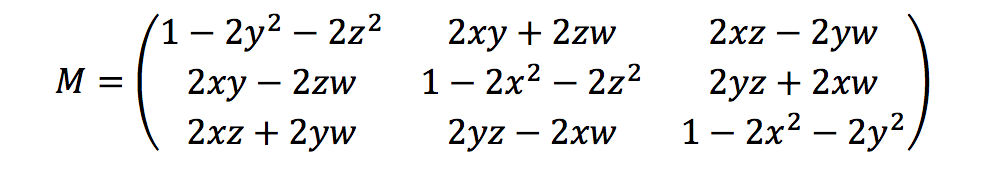
Qui, [x, y, z, w] corrisponde ai parametri dell'headingJSONoggetto,. [qx, qy, qz, qw] Ground Truth calcola il vettore della colonna di traduzione come T = [poseX, poseY, poseZ]. Quindi, i parametri estrinseci sono semplicemente i seguenti:

LiDAR_extrinsic = [R T;0 0 0 1]

Calibrazioni telecamera: estrinseca, intrinseca e distorsione

La calibrazione geometrica della telecamera, detta anche resezionamento della telecamera, stima i parametri di un obiettivo e di un sensore di immagine di un'immagine o di una telecamera. È possibile utilizzare questi parametri per correggere la distorsione dell'obiettivo, misurare la dimensione di un oggetto in unità mondiali o determinare la posizione della telecamera nella scena. I parametri della telecamera includono i coefficienti intrinseci e di distorsione.

Telecamera estrinseca

Se viene data la posa della telecamera, Ground Truth calcola la telecamera estrinseca in base a una rigida trasformazione dal piano 3D al piano della telecamera. Il calcolo è lo stesso di quello utilizzato per Li Extrinsic DAR, tranne che per il fatto che Ground Truth utilizza la posa della telecamera (position e heading) e calcola l'estrinseca inversa.

 camera_inverse_extrinsic = inv([Rc Tc;0 0 0 1]) #where Rc and Tc are camera pose components

Intrinseca e distorsione

Alcune telecamere, come le telecamere stenopeiche o fisheye, possono introdurre una distorsione significativa nelle foto. Questa distorsione può essere corretta utilizzando i coefficienti di distorsione e la lunghezza focale della telecamera. Per ulteriori informazioni, vedi Calibrazione della telecamera con OpenCV nella documentazione di OpenCV.

Ci sono due tipi di distorsione che Ground Truth può correggere: la distorsione radiale e la distorsione tangenziale.

La distorsione radiale si verifica quando i raggi di luce si piegano più vicino ai bordi di un obiettivo rispetto al suo centro ottico. Più piccolo è l'obiettivo, maggiore è la distorsione. La presenza della distorsione radiale si manifesta sotto forma di effetto barile o fish-eye e Ground Truth utilizza la Formula 1 per non distorcerla.

Formula 1:

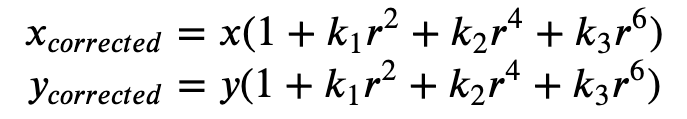
La distorsione tangenziale si verifica perché gli obiettivi utilizzati per riprendere le immagini non sono perfettamente paralleli al piano di imaging. Questo può essere corretto con la Formula 2.

Formula 2:

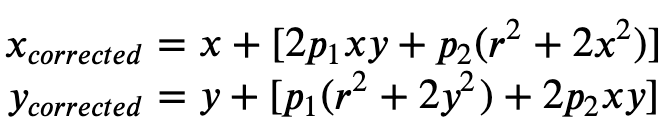
Nel file manifest di input, è possibile fornire coefficienti di distorsione e Ground Truth eliminerà la distorsione delle immagini. Tutti i coefficienti di distorsione sono in virgola mobile.

Se la distorsione delle immagini è già stata eliminata, tutti i coefficienti di distorsione dovrebbero essere 0 nel manifest di input.

Al fine di ricostruire correttamente l'immagine esatta, Ground Truth fa una conversione delle unità delle immagini in base alle lunghezze focali. Se si utilizza una lunghezza focale comune con un dato rapporto di aspetto per entrambi gli assi, ad esempio 1, nella formula superiore avremo una singola lunghezza focale. La matrice contenente questi quattro parametri è indicata come matrice di calibrazione intrinseca della telecamera.

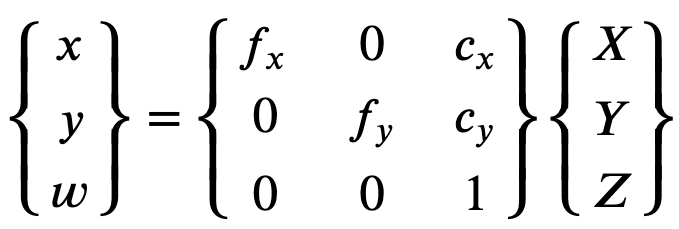
Sebbene i coefficienti di distorsione siano gli stessi indipendentemente dalle risoluzioni della telecamera utilizzate, questi dovrebbero essere scalati con la risoluzione corrente rispetto alla risoluzione calibrata.

Di seguito sono riportati i valori in virgola mobile.

Ground Truth utilizza la telecamera estrinseca e intrinseca per calcolare i parametri della vista, come mostrato nel seguente blocco di codice per trasformare le etichette tra la scena 3D e le immagini 2D.

def generate_view_matrix(intrinsic_matrix, extrinsic_matrix):
    intrinsic_matrix = np.c_[intrinsic_matrix, np.zeros(3)]
    view_matrix = np.matmul(intrinsic_matrix, extrinsic_matrix)
    view_matrix = np.insert(view_matrix, 2, np.array((0, 0, 0, 1)), 0)
    return view_matrix